摘要: 图神经网络(GNN)是一类基于深度学习的处理图域信息的方法, 它通过将图广播操作和深度学习算法结合, 可以让图的结构信息和顶点属性信息都参与到学习中, 在顶点分类、图分类、链接预测等应用中表现出良好的效果和可解释性, 已成为一种广泛应用的图分析方法. 然而现有主流的深度学习框架(如TensorFlow、PyTorch等)没有为图神经网络计算提供高效的存储支持和图上的消息传递支持, 这限制了图神经网络算法在大规模图数据上的应用. 目前已有诸多工作针对图结构的数据特点和图神经网络的计算特点, 探索了大规模图神经网络系统的设计和实现方案. 首先对图神经网络的发展进行简要概述, 总结了设计图神经网络系统需要面对的挑战; 随后对目前图神经网络系统的工作进行介绍, 从系统架构、编程模型、消息传递优化、图分区策略、通信优化等多个方面对系统进行分析; 最后使用部分已开源的图神经网络系统进行实验评估, 从精确度、性能、扩展性等多个方面验证这些系统的有效性.
关键词: 图神经网络、大规模图数据、分布式系统、深度学习、 反向传播
深度学习在对象检测[1, 2]、机器翻译[3, 4]、语音识别[5]、物理系统[6, 7]等领域取得了革命性的成功, 推动了对模式识别和数据挖掘的研究. 现有的深度学习方法能够处理欧式空间表示下的规则数据, 例如图像数据可以表示为欧几里得空间中的规则网络, 而现实中的很多应用的数据以图的形式来表示. 比如在社交网络[8]中, 可以通过图来表示对象之间的关联关系, 从而能够进行社区发现、聚类[9]等算法. 在生物领域[10], 可以通过图来表示蛋白质分子之间的关系, 从而能够对蛋白质进行分类. 在引文网络[11]领域, 可以用图来表示论文之间的引用关系, 从而能够对论文按领域进行分组. 在电子商务领域, 可以用图来表示用户和商品之间的交互关系, 从而能够对用户进行商品的推荐. 由于图数据的不规则性和稀疏性, 每个顶点可能具有不同数量的邻居, 并且图数据之间具有依赖性, 图中每个顶点的计算依赖于其他的顶点, 所以导致很多深度学习方法无法直接应用在图数据中. 例如, 卷积只能对图像或文本这样的欧几里德数据进行操作, 无法直接应用于图数据, 限制了深度学习方法在图领域的发展.
随着图领域深度学习方法逐渐受到广泛关注, 近些年出现了很多图神经网络算法, 这些方法通过在传统深度学习模型中添加图操作, 应用图的结构信息和属性信息, 来处理图数据的复杂性, 成为解决图学习问题的有效方法. 比较典型的工作有Structure2Vec[12]、GCN[13]、FastGCN[14]、AS-GCN[15]、GraphSAGE[16]等. 图神经网络算法将传统深度学习的方法, 如卷积, 扩展到了图数据领域, 并结合数据传播的思想形成了在图上的深度学习算法, 其在社交网络、推荐系统[17]、知识图谱[18]、链接预测[19]等领域都取得了良好的效果.
图神经网络受到广泛关注的原因如下: 首先, 现有标准神经网络无法正确处理图数据的输入, 因为其按照特定顺序处理节点特征, 而图中的顶点没有自然顺序. 图神经网络算法采用在顶点上传播信息的计算方式, 忽略顶点的输入顺序解决了这个问题. 第二, 在标准神经网络中, 图中顶点的依赖关系仅能作为顶点特征输入, 而图神经网络算法根据图中顶点的依赖关系进行信息传播, 保留了图结构的信息, 为下游深度学习任务提供了更加完整的信息. 第三, 推理是高级人工智能的一个重要研究课题, 图神经网络强大的表示能力, 为进一步生成强大的神经模型提供了基础.
现有的深度学习框架如TensorFlow[20]、PyTorch[21]、MXNet[22]以及CNTK[23], 和图处理框架PowerLyra[24]、PowerGraph[25]、Garaph[26]、Pregel[27]、TuX2[28]都不能很好地支持图神经网络的计算, 这阻碍了图神经网络的进一步发展, 也限制了图神经网络在大规模数据中的应用. 因此突破现有框架限制, 开发专用于图神经网络训练的系统, 对于充分发挥图神经网络的潜力十分重要.
本文首先分析图神经网络算法的计算模式, 提出大规模图神经系统训练存在的挑战, 并对现有系统进行介绍. 然后从系统架构、通信优化等多个维度对这些系统进行详细的分析和对比, 对图神经网络系统的不同优化技术进行总结和分析, 并对目前已经开源的图神经网络系统设计实验, 从多个方面测评系统的性能, 验证系统有效性.
01
图神经网络概述
早期的图神经网络研究[29, 30]基于递归的方式设计, 通过迭代地传播邻居信息直到到达不动点来学习顶点的表示. 它基于信息传播机制, 通过周期性地交换邻域信息来更新顶点的状态, 直到达到稳定的平衡为止. 每次迭代都以顶点当前的状态、顶点的特征、顶点邻居的特征和边的特征作为递归函数的输入, 该递归函数的输出用来更新顶点状态, 当状态满足收敛标准时, 会将最后一步的顶点状态输入到输出层中. 递归图神经网络交替进行顶点状态传播和参数梯度计算来训练神经网络, 根据不动点理论, 递归函数必须是一个压缩映射函数, 才有唯一不动点解, 确保收敛. 递归图神经网络启发了后来基于空间的卷积图神经网络的研究. 但由于图神经网络中每个顶点的计算依赖于该顶点的邻居, 并且递归函数在每一层的参数都是共享的, 导致这个训练过程的计算代价非常大, 所以在现实中的应用很少.
随着卷积神经网络在欧式数据上的成功应用, 比如图像分类、对象检测、机器翻译, 开始出现了图卷积的概念. CNN[31]能够学习到局部稳定的结构, 通过局部化的卷积核, 再经过层级堆叠, 把这些局部的卷积学到的结构变成层次化的多个尺度的结构模式, 构建了高度表达的表示能力, 这个能力得益于在参数共享上的设计. CNN的关键可以概括为: 本地连接、共享权重和多层的设计[32]. CNN利用平移不变性, 来对欧式数据提取特征进行分析, 而把卷积从欧式数据迁移到非欧数据的主要难点在于, 非欧数据的结构是不规则的, 例如在图数据中, 顶点的度差异很大, 在图上很难找到一个对所有顶点都适用的卷积核.
近些年提出了很多重新定义图卷积概念的方法, 主要分为两类. 基于谱方法图神经网络[13, 33-36]引入信号处理的方法, 通过将顶点特征变换到谱域实现卷积, 再将结果变换到空间域来定义图卷积, 而基于空间方法图神经网络[16, 37, 38]在节点域通过信息聚合的方法直接定义图卷积. 图卷积神经网络主要思想是通过汇总顶点自身的特征和顶点邻居的特征来生成顶点的表示形式, 与递归图神经网络不同的地方在于, 图卷积神经网络通过堆叠多个图卷积层来计算顶点表示, 在每层中使用不同的参数来解决递归图神经网络中因参数共享而导致计算代价大的问题.
谱方法将图上的信号变换到谱域, 在谱域实现图卷积的定义, 再将结果变换到空间域. 较早出现的ChebyNet是基于谱方法的图卷积神经网络, 通过将谱域的卷积核做参数化, 并利用多项式的函数对卷积核近似, 来将参数进行降维, 且不需要做特征分解, 降低了计算代价. 除此之外, 还有AGCN等, 都属于基于谱方法的图卷积神经网络.
空间方法通过图上的信息聚合来定义图卷积, 通过将中心顶点的特征和其邻居的特征进行卷积, 来更新中心顶点特征. 空间方法的图卷积运算本质上是沿着边传播顶点信息. 其中具有代表性工作的是GCN, 它既是空间方法的起点, 也是谱方法的一个特例. 其他的基于空间方法的工作还有GraphSAGE、GAT等. 通常情况下顶点邻居分布并不均匀, GraphSAGE通过对每个顶点进行固定数量邻居的采样, 然后将获得的信息进行聚合来更新顶点. GAT针对每一个顶点计算相应的隐藏信息, 通过引入注意力机制, 可以将模型应用于未知图结构的数据, 在顶点分类任务中取得了比较好的结果.
后来又发展出了许多其他类型的图神经网络, 包括图自动编码器GAE[39, 40]和时空图神经网络STGNN[41]. 图自动编码器GAE是无监督的学习框架, 可将图编码到潜在的矢量空间中, 并从编码信息中重建图数据. GAE主要用于学习网络嵌入. 时空图神经网络STGNN是一种基于时空的图神经网络, 它旨在从时空图中学习隐式的特征模式, 同时考虑顶点在时间上的依赖性和空间上的依赖性. 这种模式有多种应用, 例如交通速度预测, 驾驶员操纵预期.
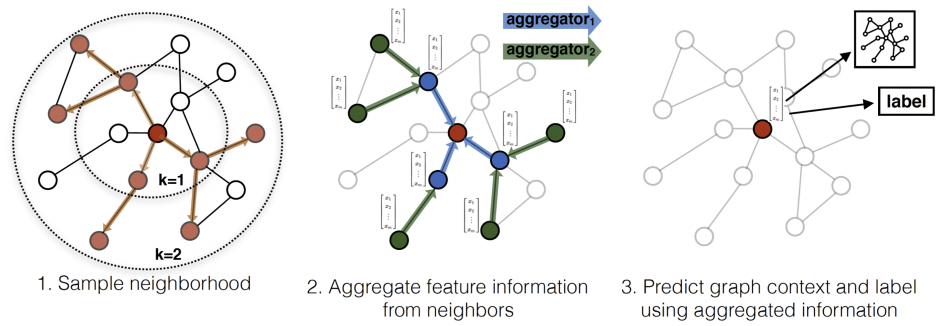
图神经网络的典型计算过程: 本文结合一种广泛应用的图神经网络模型GraphSAGE, 简要介绍图神经网络的典型计算过程. GraphSAGE是一种用于学习顶点表示的图神经网络算法, 通过对顶点邻域进行采样和聚合来生成顶点的嵌入. 其中图 , 顶点特征, 层数为K, 权重矩阵为, 非线性函数为 , 顶点v的邻居表示为 , 聚合操作为 . 如图1所示.
(1)对顶点v进行固定大小的K阶邻居采样.
(2)在顶点上进行K次聚合操作的迭代式计算. 其中, 每次计算的第k层表示由第k−1层生成.
(3)在第K次迭代中, 每个顶点v将其邻居顶点 的表示通过聚合函数聚合为单个向量,
(4)在聚合邻居顶点表示后, 将顶点当前层的表示与聚合的邻居向量连接起来, 输入到非线性激活函数中生成新的顶点表示.
(5)将顶点迭代K次后的表示作为顶点的嵌入. 若执行顶点分类任务, 可将顶点嵌入输入到Softmax层, 通过输出结果 来预测顶点分类, 最后采用交叉熵损失函数L来更新参数.
(6)在反向传播过程中, 计算第i层参数的梯度要用到第i+1层的顶点特征. 对第i层的参数 的梯度可表示为:
(7)用 的结果来更新第 层的参数矩阵, 从而完成一次训练迭代的过程. 最后重复(2)至(7)步直到参数收敛, 完成整个训练过程.
02
大规模图神经网络训练的挑战
随着图神经网络在不同领域的应用越来越广, 对训练图神经网络系统的性能要求也越来越高. 结合对图嵌入[42-44]以及图神经网络[45, 46]的分析, 本文对设计开发神经网络训练系统存在的挑战进行如下总结.
(1)现有深度学习系统不能很好地抽象图传播过程. 现有的深度学习系统处理的是规则数据, 规则数据中每个样本的计算图是独立的, 与其他样本无关, 而图神经网络是将深度神经网络和迭代图传播结合起来进行计算的, 图数据的每个样本(即图顶点)之间具有依赖性, 所以现有系统不能自然地表达和有效地支持图传播模型. 如何突破现有框架的局限, 设计一种适用于图神经网络的系统架构是发展图神经网络的重要问题;
(2)训练大规模图神经网络的计算、存储复杂度高. 真实世界中的尺寸都非常大, 而且由于顶点之间具有复杂的依赖性, 随着图神经网络层数的增加, 计算成本和内存空间需求呈指数级增长. 例如Facebook的社交网络图包含超过20亿个顶点和1万亿条边, 这种规模的图在训练时可能会产生100 TB的数据. 所以针对大图的训练, 如何设计计算和存储策略以利用有限的资源来使系统达到理想的性能也是发展图神经网络系统的一大挑战;
(3)图计算局部性差导致系统开销问题. 真实世界图的稀疏性会导致非常差的空间局部性, 在单机系统中这会导致Cache命中率降低. 而在分布式系统中, 这会导致频繁的跨节点访问, 进而产生大量的消息传递开销. 所以如何针对图的特殊性质减少系统开销是提高系统性能的一大挑战;
(4)图的幂律分布导致分布式计算负载均衡问题. 对于具有数亿个顶点的大型图, 通常需要对图进行分布式处理, 图神经网络算法不同于传统的图算法, 平衡的图分区不仅依赖于分区内的顶点数量, 还依赖于分区内顶点邻居的数量, 多层图神经网络模型中不同顶点多阶邻居的数量可能相差极大, 并且这些分区之间需要频繁的数据交换, 如何对图数据进行合理的分区来保证分布式训练的性能是对于分布式系统的重大挑战;
(5)异构计算架构中的任务划分和负载调度的合理性问题. GPU的广泛应用为训练深度学习模型带来了很多机会和挑战. 在利用GPU加速神经网络的训练时, 通常将数据存储在主机内存中, 在计算时需要将数据传输到GPU, 由于图神经网络算法在反向传播阶段的复杂性, 需要频繁的在主机和GPU之间进行数据传输, 如何设计合理的调度方案来最大程度地减少数据传输成本也是提高系统性能的一大挑战.
为了应对这些挑战, 出现了很多针对图神经网络的训练框架, 其中单机系统如PyTorch Geomertic、DGL、NeuGraph. 图神经网络通常处理非常大且不规则的图, 这些大图无法存储在单个设备中, 因此必须以分布式方式进行分区和处理, 其中分布式图神经网络框架如Euler、AliGraph、Roc、AGL. 接下来本文将介绍若干典型的单机图神经网络系统以及分布式图神经网络系统.
03
图神经网络系统介绍
图神经网络算法将深度神经网络的运算(如卷积、梯度计算)与迭代图传播结合在一起: 每个顶点的特征都是由其邻居顶点的特征结合一组深度神经网络来计算. 但是, 现有的深度学习框架不能扩展和执行图传播模型, 因此缺乏高效训练图神经网络的能力, 并且现有框架一般采用数据/模型并行来分布式训练深度神经网络, 这种并行计算方法难以直接应用于图神经网络, 因此限制了训练大规模图神经网络的能力. 而现有的图处理系统虽然能够表示迭代图传播模型, 并能有效支持大规模图的迭代计算, 但是缺乏支持神经网络计算的关键能力, 如张量抽象、自动微分等. 因此, 为了支持图神经网络在大规模图上的应用, 以及对更复杂图神经网络结构的探索, 开发针对图神经网络的训练系统是十分有必要的.
目前具有代表性的图神经网络框架: DGL[47]、PyTorch Geometric[48]、NeuGraph[49]、EnGN[50]、Euler[51]、PSGraph[52]、AliGraph[53]、Roc[54]、AGL[55]、PGL[56]. DGL[47]是易于使用, 高性能且可扩展的Python库, 用于图结构的深度学习, 能够与主流的深度学习框架集成, 例如Tensorflow[20]、PyTorch[21]、MXNet[22]. PyTorch Geometric[48]是基于PyTorch构建的深度学习库, 用于处理非结构化数据的深度学习. NeuGraph[49]是一种将数据流系统和图处理系统结合起来训练图神经网络的框架, 它构建在现有的数据流引擎之上, 使用Python和C++作为开发语言. EnGN[50]是一种以边为中心, 专门用于大规模图神经网络训练的加速器. Euler[51]与PSGraph[52]是一个与深度学习工具集成的大规模分布式图学习框架, 支持用户在数十亿点数百亿边的图上进行模型训练. AliGraph[53]是由阿里巴巴团队开发的采样建模训练一体化的图神经网络平台. Roc[54]是一种用于快速图神经网络训练的分布式多GPU框架. AGL[55]是用于工业用途图学习的集成系统, 利用传统基础架构(MapReduce、参数服务器[57])实现了容错性和一致性. PGL (paddle graph learning)[56]是由百度开发的基于PaddlePaddle的高效灵活的图学习框架.
3.1 DGL
DGL是用于图结构深度学习的Python库, 通过与主流的深度学习框架集成, 能够实现从传统的张量运算到图运算的自由转换. DGL提供基于消息传递的编程模型来完成图上的计算, 结合消息融合等优化技术使系统达到了比较好的性能.
DGL的API主要有两部分, 一是消息函数:
二是累和函数:
其中, ek代表边k的属性向量, vi代表顶点i的属性向量, vrk是边k的源顶点属性向量, vsk是边k的目的顶点属性向量, mk代表边k上的消息, t代表迭代次数. 是一个消息函数, 定义在边上, 通过将边的特征与两端的顶点特征组合来生成“消息”. 是在每个顶点上定义的更新函数, 通过使用reduce操作汇总其传入的消息来更新顶点特征. 在图神经网络中, 这些功能由神经网络模块进行参数化, 可以是求和运算, 也可以是均值, 最大值、最小值或LSTM网络, s.t. rk=i表示对目的顶点为i的所有消息进行聚合操作.
消息张量的大小正比于图中边的数量, 因而当图增大时, 消息张量消耗的内存空间也会显著上升. 为了避免生成消息张量带来的额外存储开销, DGL实现了消息融合技术, 将send函数和recv函数合并成了 .
3.2 PyTorch Geometric
PyTorch Geometric, 是一个基于PyTorch构建的深度学习库, 可以对非结构化数据进行建模和训练. 该库利用专用CUDA内核实现了高性能训练. PyTorch Geometric提供一个简单的消息传递API, 将卷积算子推广到不规则域, 具体表示为:
其中, 表示可微置换不变函数, 如求和、均值或最大值. 整个模型可以通过gather和scatter顶点特征以及对其进行矢量化的元素计算来实现. 通过这个消息传递模型, 用户只需要定义消息函数和更新函数, 以及选择聚合方案 , 就可以设计新的图神经网络模型. 该库采用COO格式编码边索引, 一个维度表示源顶点, 另一个维度表示目标顶点, 这种存储格式非常适用于消息传递模型, 能够快速获取顶点对应的源顶点的信息. 与通过矩阵乘法实现的方法相比, 使用消息传递模型能够达到更好的性能.
3.3 NeuGraph
NeuGraph提出了一种新的框架, 根据图神经网络是将标准神经网络与迭代图传播结合起来的这一特点, NeuGraph在数据流中引入以顶点为中心的消息传递模型, 将图模型和数据流模型结合, 来支持并行图神经网络计算. NeuGraph还将图计算的优化方法如数据分区、调度, 引入到了数据流框架中, 来支持高效的图神经网络训练.
NeuGraph提出了一种新的处理模型SAGA-NN, 它将数据流和顶点编程模式相结合来表示图神经网络的计算. SAGA-NN将前向计算分为4个阶段: Scatter、ApplyEdge、Gather和ApplyVertex. ApplyEdge和ApplyVertex提供了两个用户定义函数, 供用户在边和顶点上声明神经网络计算. ApplyEdge函数定义每个边上的计算, 以edge和W作为输入, 其中edge是指边数据, W包含图神经网络模型的可学习参数. ApplyVertex函数定义了顶点的计算, 它以顶点张量、顶点聚合累积量和可学习参数W作为输入, 并在应用神经网络模型后返回新的顶点表示. Scatter和Gather执行数据传播和收集, 由系统隐式触发和执行. SAGA-NN中的顶点程序采用以顶点为中心的编程模型来表达图神经网络的计算, 对图神经网络中的通用阶段进行建模, 并在图计算和数据流调度中实现优化.
NeuGraph在数据流抽象的基础上引入了特定的图分区方法, 可以解决GPU内存的物理限制问题. 通过2D图分区方法, NeuGraph将顶点数据分割成P个大小相等的不相交顶点块, 并将邻接矩阵分为P×P个边块. 通过将图数据分割成块, 在逐个处理边块信息时, 只需要边块所对应的源顶点块和目标顶点块即可. 在训练过程中, 与顶点块或边块相关的一些中间特征数据将用于反向传播. 为了节省GPU内存, 它们在前向计算期间交换到主机内存, 在反向传播期间交换回. NeuGraph为降低主机和GPU内存之间的数据传输做了一系列优化: 在处理边块E时, NeuGraph设计了一个过滤器, 来过滤每个顶点块内的必要顶点, 并将其传输到GPU中; 通过一种局部感知的图划分算法, NeuGraph将连接同一顶点的边尽可能地压缩到一个块内, 通过这种方法, NeuGraph可以获得更好的顶点数据访问局部; NeuGraph设计流水线调度进一步重叠数据传输和计算, 以隐藏传输延迟.
3.4 EnGN
EnGN是一种处理大规模图神经网络的专用加速器架构, 并且EnGN提出了一种使用专用架构的以边为中心的数据流模型. EnGN将常见的图神经网络计算模式抽象为特征提取, 聚合和更新3个阶段. 在特征提取阶段, 神经网络来压缩图中每个顶点的属性. 聚合阶段通过聚合在特征提取中生成的每个顶点的邻居属性, 来产生统一的输出特征, 其中聚合函数的选择包括各种算术运算, 例如max, min和add. 在传播迭代结束时, 更新阶段会利用学习到的参数进一步压缩聚合阶段中获得的输出特征, 并在输出之前将非线性激活函数或GRU/LSTM函数应用于图的每个顶点.
在以边为中心的数据路模型基础上, EnGN集成了一个神经图处理单元(NGPU), 能够在统一的体系结构中执行特征提取, 聚合和更新操作. 它具有一个PE数组, 每个PE单元都包含一个本地寄存器, 用于存储临时结果并充当PE间通信的中介. EnGN提出了图属性感知(GPA)数据流, 来分离顶点的输入属性和硬件计算结构. 以这种方式, PE阵列的同一列中的每个PE负责顶点属性的单个维, 而同一行中的每个PE处理单个顶点. 输入顶点属性的尺寸变得独立于硬件体系结构, 并且可以连续地注入到PE阵列中, 而与阵列大小和属性尺寸无关. 通过这种方式, 处理单元可以处理具有任意尺寸属性的顶点. RER (ring-edge-reduce)阵列同一列中的每个PE连接到环形网络中的邻居, 同一列中的每个PE仅与其两个最近的邻居(北, 南)通信. PE将其数据发送到北部邻居, 并接收从南部邻居发送的数据以进行汇总. 以此方式, PE可以基于环型数据流从边解析的控制信号来选择要聚合的相关顶点.
3.5 Euler
Euler是集成了深度学习系统TensorFlow的基于CPU的分布式图神经网络框架, 支持图分割和高效稳定的分布式训练, 可以轻松支持数十亿点、数百亿边的计算规模.
Euler系统抽象为图引擎、图操作算子、算法实现3个部分, 可以快速地扩展一个图学习算法. 该系统整体可以分为3层: 最底层的分布式图引擎, 中间层图语义的算子, 高层的图表示学习算法. 在底层图引擎部分, Euler采用了分布式存储的架构, 整个图在引擎内部用哈希方法切分为多个子图, 每个计算节点被分配一个或几个子图. 在进行迭代图广播时, 顶层操作被分解为多个对子图的操作, 并由各个计算节点并行执行, 充分利用了各个计算节点的计算能力. 在中间层Euler提供了多种图操作的算子, 如全局带权采样点和边, 基于给定顶点的邻居操作等等. 利用灵活的图操作算子, Euler不仅支持传统的以图为中心的学习模式, 且可以把基于图的学习方法结合到传统的学习任务中, 实现端到端训练. Euler在算法层内置了多种常见算法以及几种创新算法, 如Scalable-GCN, 一种加速GCN训练的方法.
3.6 AliGraph
AliGraph是由阿里巴巴开发的图神经网络系统, AliGraph总体上由5层组成, 如图2[53], 其中存储层、采样层和操作层构成了系统的基础, 算法层和应用层构建在前3层的基础之上. 其中存储层应用了多种技术来存储大规模原始图数据, 以满足多种图操作和算法对快速数据访问的要求, 即结构化存储和属性特定存储, 图分区和某些重要顶点邻居的缓存. 在采样层Aligraph对采样操作进行了有针对性的优化, 将采样方法分为Traverse, Neighborhood和Negative这3类, 并提出了一种无锁方法来在分布式环境中执行采样操作. 运算符层提供了Aggregate和Combine等常见运算符的优化实现.
AliGraph建立在分布式环境中, 因此整个图被划分并分别存储在不同的节点中. 图分区的目标是最大程度地减少顶点在不同计算节点中的交叉边的数量. 系统实现了4种内置的图形分区算法: METIS、顶点切割和边缘切割分区、二维分区、流式分区策略. 除此之外, 为了进一步降低通信开销, AliGraph提出了一种在本地缓存重要顶点邻居的优化方法, 但顶点邻居过多会导致存储成本增加. 通过对顶点重要程度的度量, AliGraph可以在通信成本和存储成本之间做到很好的平衡. 并且AliGraph证明了只需要缓存少量重要顶点即可实现通信成本的显著降低.
3.7 Roc
Roc是用于快速图神经网络训练的分布式多GPU框架. 其性能提升得益于Roc的图分区和内存管理优化实现. 系统利用多计算节点多GPU的计算资源在完整的现实世界图上训练大型图神经网络模型, 来达到更好的性能和可扩展性.
图神经网络算法将计算密集型深度神经网络操作与数据密集型图传播混合在一起, 因此在分布式环境中实现负载均衡的图分区是非常困难的. Roc使用在线线性回归模型来对图分区进行建模. 在图神经网络架构的训练阶段, Roc建立了一种成本模型, 用于预测在输入图上执行图神经网络操作的执行时间, 成本模型既包含与图相关的部分, 如图中顶点和边的数量, 也包含与硬件相关的部分, 如执行该操作的GPU内存访问的次数. 在图神经网络的每次训练迭代期间, Roc使用成本模型来预测计算图分区, 并使用图分区的结果来并行化训练. 在每次训练迭代结束时, 子图的实际运行时间将发送回Roc图分区模块, 该程序通过最小化实际运行时间与预测运行时间之间的差异来更新成本模型. Roc还将GPU内存管理形式化为成本最小化问题: 给定输入图, 图神经网络结构和GPU设备, 找到张量子集以缓存在GPU内存中, 最大程度地减少CPU和GPU之间的数据传输. 为了快速求解成本模型, Roc引入了动态规划算法以快速找到全局最优解.
3.8 PSGraph
PSGraph使用Spark和PyTorch作为资源管理和计算平台, 使用参数服务器架构作为分布式训练架构. PSGraph通过参数服务器为Spark提供支持, 以有效地训练数十亿规模的图数据, 并将PyTorch集成到Spark中来实现神经网络的训练.
PSGraph由参数服务器、计算引擎和主节点构成. 参数服务器用于存储高维数据和模型, 它支持不同的数据结构, 除此之外, PSGraph还为用户提供实现新数据结构的接口, 支持按行索引和列索引的数据分区方式, 提供不同的同步协议以控制工作进程之间的同步, 以及实现多种常用运算符来操作参数服务器上的数据, 每个参数服务器定期将本地数据分区存储到HDFS. 计算引擎由Spark和PyTorch实现, 用于存储数据、计算并创建参数服务器代理来管理Spark和参数服务器之间的数据通信. 主节点负责资源分配、任务监视和故障恢复.

3.9 AGL
AGL是用于工业用途图学习的集成系统. 在AGL系统中图神经网络的计算构建于消息传递模型基础之上, 其迭代图传播过程使用MapReduce来实现. 在训练图神经网络阶段, AGL通过构造k-hop邻域, 来提供信息完整的子图, 通过从边合并邻居的消息来计算每个顶点的嵌入. AGL将原始图分解成子图, 来使每个顶点的计算图可以独立于其他顶点.
AGL的核心有3个模块: GraphFlat, GraphTrainer和GraphInfer. GraphFlat是基于消息传递的高效分布式图生成器, 用于生成顶点的K阶邻域信息, K阶邻域信息包含每个目标顶点完整K阶子图和所有顶点的属性信息. 由于K阶邻域包含训练每个目标顶点的所有信息, 因此AGL可以选择将其中一部分而不是整个图加载到内存中, 从而实现完全的并行计算. GraphTrainer利用许多技术来减少I/O的开销, 并在训练图神经网络模型期间优化浮点计算, 在实际工业场景中能获得较高的近线性加速. GraphInfer, 这是一个分布式推断模块, 可将K层图神经网络模型分成K个切片, 并基于MapReduce的计算模式来完成高效的预测推理.
3.10 PGL
PGL是由百度开发的基于PaddlePaddle的高效灵活的图学习框架. PGL实现了高度并行的图神经网络消息传递机制, 并依托于自研的分布式图引擎以及大规模参数服务器PaddleFleet, 可以支持十亿节点百亿边的超大规模图训练.
PGL总体上由3层组成, 最底层分布式图引擎、分布式图训练模块以及分布式参数服务器PaddleFleet. 底层分布式图引擎以图切片的形式存储超大规模图, 提供图信息访问、子图采样等操作算子, 由上层模型调用. PGL预置了丰富的图学习模型, 这些模型涵盖了同构与异构、图表示学习与图神经网络等样例. 分布式参数服务器PaddleFleet提供了一种高效的参数更新策略: GeoSSD, 在全异步的条件下进行参数更新, 降低了节点间通信对训练速度的影响.
PGL采用类似于DGL的消息传递范式构建图神经网络的接口, 能够帮助用户快速构建自定义图神经网络, 用户只需要编写send和recv函数即可. 目前, PGL提供两种聚合方法. 一种是Scatter-Gather, 用于常规聚合计算. 另一种是基于LodTensor特性实现的并行通用的消息聚合方法. PGL将消息组织为PaddlePaddle中的LodTensor, 将消息作为可变长度序列进行拼接, 并引入一个索引数据结构来记录张量序列, 利用LodTensor的特性可以快速的执行并行聚合. 此外, PGL还支持异构图学习, 可以对包含多个节点类型和多个边类型的异构图进行建模, 并且可以描述不同类型之间的复杂连接.
04
图神经网络系统总结和分析
本节从系统架构、处理模型、图分区策略、通信优化策略、以及社区活跃度与系统易用性方面, 对现有图神经网络系统进行分析和对比, 并从多个维度对系统的特点进行总结, 以表格的形式清晰的展示系统的共性与不同, 来为研究人员提供有效参考.
(1)系统架构. DGL和PyTorch Geometric都是结合现有的深度学习框架来实现的, 并且针对图神经网络的特点做了多种优化, 达到了很好的性能. 结合现有深度学习框架来实现的系统, 更加方便用户使用, 能够帮助其更快地实现图神经网络模型. 但结合现有深度学习框架来实现的系统, 在针对图操作的优化上有很多局限性. NeuGraph采用了一种新的架构, 将图模型和数据流模型结合起来, 以支持高效的图神经网络训练, 这种架构既弥补了现有数据流引擎不能有效地支持图计算的缺点, 又弥补了图引擎不能支持数据流编程模型的缺点. EnGN在统一的处理模型基础上, 开发了一个定制的EnGN加速器, 它集成了一个神经图处理单元(NGPU), 可以在统一的体系结构中执行特征提取, 聚合和更新操作. EnGN的专用加速器突破了硬件结构的限制, 相比于其他系统配备的多个CPU或GPU, 大大降低了成本和能源开销. AliGraph、Euler和PGL的架构类似, 都采用分层架构, 构建于现有数据流框架之上, 并且都构建在CPU平台上. Roc将图神经网络的计算分布在多个计算节点上, 每个计算节点可以包含多个GPU, 每个计算节点在子图上执行图神经网络的训练, 并与CPU通信来获得输入张量并保存中间结果. Roc采用分布式多GPU的架构不仅解决了单节点系统对于大规模图的限制, 并且比基于CPU的系统更高效. AGL、PSGraph都是利用现有大数据处理系统和参数服务器的并行体系结构来组建的基于CPU的分布式图神经网络训练框架, 这些系统具有良好的容错性和可伸缩性.
(2)处理模型. DGL和PyTorch Geometric通过使用面向图的消息传递接口包装深度学习系统, 来支持针对图神经网络的编程. 这种消息传递模型很好地表示了图上的数据流动, 整个模型分为两步. 第1步: “消息”生成操作, 这个操作定义在每个边上, 通过将边的特征与两端顶点特征组合为每一条边生成一条“消息”. 第2步: 更新操作, 定义在每个顶点上, 通过汇总顶点入边传入的消息来更新顶点特征. 通过系统提供的消息传递接口, 用户可以快速实现图神经网络的原型制作. PGL也采用消息传递范式构建图神经网络的接口, 并提供多种聚合方法, 提高了并行处理效率. NeuGraph提出了一种新的处理模型SAGA-NN, 提高了在顶点和边上执行批量操作的灵活性, 提供了在图计算和数据流调度中实现优化的机会, 提高了系统性能. EnGN提供一种以边为中心的处理模型, 将图神经网络的计算抽象为特征提取, 聚合和更新3个阶段. EnGN与其他3个系统不同, 在处理模型基础上定制了针对图神经网络的加速器, 不依赖于现有的深度学习系统, 并拥有独特的数据流处理方法. EnGN优化了顶点数据和边数据移动的内存访问模式. 对于大图中的源顶点数据访问, 采用图切片技术, 并确保对源节点的访问仅引起对连续内存地址的访问. 对于聚合和更新阶段中的随机目标顶点访问, EnGN利用哈希边数据布局和多级缓存方法来避免写冲突并提高片上缓冲器中的数据命中率.
(3)图分区策略. 平衡的图分区是实现分布式图神经网络系统的关键之一. Euler采用简单的哈希方法将图的顶点进行分片, 这种分片方式使各个节点拥有目标顶点的数量基本一致, 但是在每个顶点的子图中拥有的邻居数量是不同的, 所以每个节点的计算负载并不均衡. AliGraph则提供了多种内置的图分区算法供用户选择, 比如适合处理稀疏图的METIS方法, 适合稠密图的点割和边割方法, 这种方法虽然为用户提供了多种选择, 但需要用户自己去判断使用哪种分区方式, 给用户造成很大不便. Roc采用一种在线线性回归模型来优化图分区. 这种基于线性回归的图分区方法在图神经网络系统中能够达到比传统分区更好的性能.
(4)通信优化策略. 针对通信开销影响分布式系统性能的问题, Euler采用的是缓存对应顶点k阶内的邻居顶点信息, 这种方式虽然直接避免了计算节点之间的通信, 但是造成了很严重的内存浪费, 并且在幂律分布的图中还会使各个计算节点之间负载不均衡. AGL采用的策略和Euler相同, 但是AGL提出了重新索引的策略来均衡负载. AliGraph提出了一种缓存重要顶点的邻居的方法来降低通信开销, 同时提出了一种对顶点重要性的度量标准, 既能有效减低通信开销, 又防止产生巨大的存储成本, 避免资源浪费. ROC引入了代价模型, 可以最大程度地减少CPU和GPU之间的数据传输. 这种动态的方法突破了手动优化的局限, 将影响通信的多种因素综合考虑, 从而更好的降低通信成本, 提高系统性能. PGL的分布式参数服务器提供了一种高效的参数更新策略: GeoSSD, 在全异步的条件下进行参数更新, 并重叠模型训练与节点通信, 在保证模型效果的前提下提升了训练效率.
(5)社区活跃度与系统易用性. PyTorch Geometric、DGL、AliGraph、Euler、PSGraph、PGL为开源系统, 这里的社区活跃度以GitHub上讨论区的数量为标准, 这其中最活跃的社区为PyTorch Geometric. 在系统易用性方面, 从配置文件的完整度、对其他系统的依赖度、用户使用的方便度多个角度综合考量, 这其中DGL和PyTorch Geometric的易用性排在前列, 而Euler与PSGraph虽然给出了配置文件, 但在配置系统时, 需要配置其他多个依赖包, 并且数据处理过程繁琐, 不易用户使用. 本文为系统的社区活跃度和易用性给出星级评价, 星级越高, 系统在这两方面表现越好, 其中空白符号表示系统未开源.
本文对目前的图神经网络系统从多个维度进行了综合分析, 对这些系统的共同特性进行提取, 并总结归纳, 见表1.
05
主要优化技术总结
本节结合系统特点, 对现有系统所采用的优化技术进行总结和分析, 并将优化技术汇总分类, 详细阐述具体优化技术的实施方案. 在本节最后, 对目前训练大规模图神经网络存在的挑战、具体优化方案、图神经网络系统三者之间的关联关系做出详细解释, 表明了现有的优化技术是如何解决目前存在的挑战, 以及这些优化技术被哪些系统所采用.
5.1 图神经网络的并行计算方法
图神经网络的并行计算方式与其他深度学习方法的计算方式不同. 首先, 图神经网络的计算具有顶点依赖性, 以卷积图神经网络为例, 对于一个图, 图卷积网络采用图卷积运算逐层的获取顶点的信息, 在每一层, 要获取一个顶点的表示, 需要通过采集邻居顶点的信息, 然后进行线性变换. 图3是一个两层卷积图神经网络的示意图, 其中红色顶点是将用于最终任务的顶点. 通常情况下, 神经网络的每个样本都可以作为单独的项独立训练, 而图神经网络的计算不同, 每个顶点的计算依赖于大量的其他顶点, 尤其是当层数变深时, 依赖变得更加复杂. 针对图神经网络的并行计算方法根据不同情况有所不同.
第1种是小批量训练方法的并行计算方法. 这种训练方法通过对目标顶点进行一阶或多阶邻居的采样, 将训练目标顶点所需要的每层邻居都采样到内存中, 然后计算目标顶点的表示并用于最终任务. 这种计算方法会造成大量的计算开销和内存开销, 但其通过采样将整张图上的计算分解为多个独立的计算任务,从而为并行计算提供了可能. 如图4所示大规模c程序设计 pdf, 将原来图中的顶点按一定方式分配到不同计算节点中, 假设顶点1被分配到计算节点1中, 顶点2被分配到计算节点2中, 之后分别对顶点进行二阶邻居采样并训练, 此时计算节点中只需要存储被分配的顶点的二阶邻居即可, 并且不同计算节点之间不需要消息通信, 只需要和参数服务器进行参数的传递. 这种并行计算方法被很多大规模系统所采用, 如AliGraph、Euler、PGL, 通过结合现有数据流框架并提供高效图操作来加速图神经网络的训练, 不需要考虑神经网络的反向传播与计算节点通信, 易于系统实现并进行扩展.
第2种是利用图数据流的并行计算方法. 这种方法将图处理的方式引入到图神经网络的并行计算中, 首先将图的边信息, 即图的邻接矩阵进行分块处理, 在并行处理边的信息块时, 引入边对应的源顶点信息和目标顶点信息来计算边上的中间信息, 然后根据边对应的目的顶点对中间信息进行聚合计算, 在处理完所有边块之后再对聚合的结果进行变换, 并将输出结果作为下一层新的顶点特征. 图5展示了更新顶点块V0的计算过程, 首先将邻接矩阵A进行分块, 边块Aij中的边分别连接两个顶点块Vi和Vj中的顶点, Scatter阶段并行计算边块A00, A10, A20上对应的中间信息, Gather阶段以顶点块V0为目的顶点对生成的中间信息进行聚合, Update阶段对顶点块进行变换和更新. 这种并行计算方法被很多系统使用, 如NeuGraph, 适用于结合图数据流处理方式对框架进行扩展的系统, 能够更好地表达图神经网络的图传播操作部分. 这种计算方式与传统的图计算的一些不同在于: 1)处理的数据是多维特征; 2)由于需要反向传播计算, 因此需要保存计算的中间结果以便在反向传播中使用.
第3种是基于MapReduce模型的并行计算方法. 计算过程如图6所示, 在Map阶段生成3种信息, 顶点自身信息, 顶点入边信息及对应的邻居节点特征, 顶点出边信息, 这3种信息的key值都为顶点编号, value值为对应的信息. 按顶点编号进行Shuffle后, 在Reduce阶段, 首先将顶点自身信息和顶点入边信息以及对应邻居信息进行合并, 形成新的顶点信息, 新的顶点信息被传播到出边上用来构造新的出边信息. 在k次Reduce阶段后, 顶点的自身信息就是k阶邻域信息. 最后将信息存储起来用于下游的计算任务. 这种并行计算方法被系统AGL采用, AGL是结合MapReduce来完成迭代图传播过程的系统, 由于MapReduce本身处理大规模数据的特性, 更适用于工业用途的图学习. AGL基于成熟的工业基础架构MapReduce、参数服务器来设计系统结构, 这种方案易于部署, 同时具有容错能力.
5.2 消息融合技术
在处理图神经网络的计算时, 一种广泛采用的思路是先将源顶点的信息发送到边上, 在边上结合边自身的信息生成中间消息, 最后由目的顶点将对应的中间消息进行聚合, 并结合自身信息输入到神经网络中进行计算生成新的顶点表示. 但是通常情况下, 图中的顶点的邻居不止一个, 因此边的数量会远远多于顶点的数量, 所以生成的中间消息的数量急剧增大, 当图增大时, 中间消息消耗的内存空间也会显著上升, 这会导致计算效率的降低和计算资源利用率的下降.
在大多数图神经网络算法中, 边上的函数通常是元素级操作, 例如GCN算法在边上的操作是乘法, 乘法操作的变量是边对应的两个顶点的度, 在这种情况下, 对于每个目的顶点, 可以使用乘法对指向目的顶点的边进行GCN算法相应的操作, 将生成的结果直接累加到目的顶点上, 最后根据目的顶点的最终结果进行计算和更新, 这种计算方式无需消耗任何额外成本来创建和维护中间消息. 图7所示, 这种优化方法被很多系统采纳, 如DGL、NeuGraph, 这两个系统都采用了单机多卡的处理架构, 利用GPU来加速图神经网络的训练, DGL的核融合与NeuGraph的SAG融合都利用避免生成中间消息的方法来减少内存消耗. 消息融合方法非常适用于GPU加速, 因为GPU的存储容量有限, 消息融合技术降低了内存消耗, 同时也提高了GPU系统的吞吐量.
5.3 最小化数据移动技术
在分布式计算图神经网络时, 进行图分区后会把所有子图都发送到不同的计算节点, 然后并行执行图神经网络的计算. 对图神经网络的训练, 通常需要用GPU来进行加速, 但是GPU的内存通常比较小, 为了支持大规模的图, 不需要将与每个子图相关的所有中间结果都放入GPU内存中, 而是使用空间较大的主存来保存所有数据, GPU用来计算并起到缓存部分数据的作用. 但是, 在GPU和主机之间传输数据会对运行时性能产生影响, 所以应该以最大程度地减少数据传输. 一种最直接的策略就是缓存, 通过在GPU端缓存一部分数据信息来避免重复的数据传输. 那么, 如何执行缓存策略来使数据移动产生的开销最小, 更进一步, 如何利用除了直接缓存以外的方式来进一步减少数据移动.
利用调度方式来减少数据移动[50]. 在分布式图神经网络计算任务中, 通常需要对图数据进行切分, 最直观的方法是直接对图的邻接矩阵进行2D划分, 并相应的将顶点的特征矩阵进行切分. 邻接矩阵的行对应的是源顶点, 列对应的是目标顶点, 图8(a)给出了前馈计算的过程, 数据从源顶点流向目标顶点, 此时应该采用面向列的调度方式, 即沿着列方向处理邻接矩阵信息, 并传输对应顶点的特征矩阵, 在前馈计算中采用这种方式可以在GPU内存中重用目标顶点块和相应的累积顶点数据块, 从而最小化数据移动. 相比之下, 对于反向计算, 如图8(b)所示, 顶点梯度从目标顶点传播到源顶点, 在这种情况下, 应该采用面向行的调度方式, 即沿着行的方向处理邻接矩阵信息时, 采用这种方式可以在GPU内存中重用顶点梯度数据块. 在此行列交替调度边信息方式的基础上, 可以继续对顶点特征矩阵进行优化. 在每次利用行信息调度相应顶点块时, 并不是所有顶点块中的顶点都会被使用, 因此, 可以在主机中应用一个过滤器, 从邻接矩阵对应的源顶点块中选择有用的顶点, 并只将所选择的顶点数据传输到GPU, 来进一步减少数据移动带来的开销. 系统NeuGraph采用的是上述基于行列交替调度的方式, 来最大化的重用顶点块减少数据移动. 调度方式不仅可以减少数据移动, 还可以提高计算效率, 系统EnGN通过设定边的调度顺序, 来使聚合计算的效率最大化.
利用动态内存管理来减少数据移动[55]. Roc是多机多卡的处理架构, 需要在主机内存和GPU之间频繁交换信息, Roc采用一种动态编程算法, 对内存进行动态管理来降低传输成本. 在训练图神经网络时, 即使要计算单个顶点, 也可能需要访问其他设备和计算节点的大量相邻顶点, 这些数据传输对整体性能有很大影响. 因此, 必须决定每个中间张量应该存储在主机内存还是GPU中, 以最大程度地减少数据传输成本. 如何选择此张量子集以最大程度地减少有限GPU内存中的数据传输是一个关键的内存管理问题. 最佳策略不仅取决于GPU设备的存储容量以及输入图和图神经网络张量的大小, 还取决于图神经网络体系结构的拓扑. 通过将内存管理问题形式化为为数据传输成本最小化问题, 并使用动态规划算法进行求解. 这样一来在计算的每个阶段, 只需要考虑缓存那些将在以后的操作中重新使用的张量. 执行当前状态操作的数据传输成本为操作所需传输的不在GPU内存中的张量加上上一个状态所需的成本, 通过枚举每个运行状态下的最后一个操作, 将传输成本压缩到最小. 内存管理很难手动优化, 因为最佳策略取决于输入图的大小和拓扑结构以及如内存容量之类的设备约束. 将优化数据传输的任务表述为成本最小化问题可以最大化的提升数据传输效率.
5.4 缓存技术
通常真实世界图数据往往服从幂律分布, 所以不同顶点的访问频率差异会很大, 高阶顶点的访问频率可能是低阶顶点访问频率的数百倍甚至上千倍, 这会导致严重的访问不平衡问题, 而图神经网络的计算依赖于顶点的邻居, 所以对于高阶顶点的邻居的访问频率也会随之上升. 在分布式情况下, 频繁的访问会带来大量的通信开销, 并且高阶顶点的邻居通常数量庞大, 通过高阶顶点来访问其邻居的开销会严重影响系统的性能, 降低训练效率.
目前一种直接的想法是在每个计算节点中, 在本地缓存一些重要顶点的邻居来降低通信成本[54]. 如果顶点v经常被其他顶点访问, 可以将v的邻居存储在它出现的每个分区中. 这样, 可以极大地减少其他顶点通过v到达它的邻居的访问成本. 但是, 如果v的邻居数量很大, 则存储v的邻居的多个副本也将产生巨大的存储成本. 为了进行更好的权衡, 可以定义一个度量来评估每个顶点的重要性, 从而确定一个顶点是否值得缓存.
AliGraph提出将顶点v在k阶内的入度邻居数量和出度邻居数量的比值, 作为衡量顶点是否值得被缓存的标准, 入度邻居数量反应了顶点v被访问的频率, 而出度邻居数量衡量了缓存顶点v所产生的存储成本, 所以两个数值的比值大于一个特定的阈值时, 顶点就值得被缓存. 目前已有实验证明, 在阈值为0.2的情况下, 能在缓存成本和减少通信开销之间取得最佳平衡[54]. 并且, 有实验证明顶点的重要性值也服从幂律分布, 图中只有极少数的顶点达到重要性标准. 这意味着只需要缓存少量重要顶点即可实现通信开销的显著降低.
5.5 图分区技术
在图神经网络的训练中, GPU的有效利用对于提升性能至关重要, 特别是对于大型图. 由于GPU内存的物理限制, 大图数据往往无法全部加载到GPU存储器, 因此可以将图的顶点信息和边信息进行切分. 2D图划分是一种特定于图的分区方式, 通过将图数据分割成块, 可以对信息进行分批处理. 对于每一个边数据块, 首先输入其对应的原顶点属性和目的顶点属性块, 然后根据算法对边块对应的顶点信息进行计算并生成中间数据块, 最后再根据目的顶点对中间数据块进行聚合计算生成新的顶点数据块. 除了该种图划分方法, 顶点切割分区、边缘切割分区和流式分区都是可以应用于图神经网络的分区策略.
图神经网络将计算密集型的深度神经网络与数据密集型的图传播操作混合在一起, 并且顶点计算具有依赖性, 每个顶点的计算负载不一样, 使得在分布式情况下难以静态计算良好的负载平衡分区. Roc采用的在线线性回归模型可以用于优化图分区. 在图神经网络系统的训练阶段, 学习一种成本模型, 用于预测在输入图上执行图神经网络操作的执行时间. 为了获得执行图神经网络操作的运行时性能, 成本模型既包含与图相关的特征, 如图中顶点和边的数量, 也包含与硬件相关的特征, 如执行该操作的GPU内存访问次数. 在训练迭代期间, Roc使用成本模型中的预测结果来计算新的图分区, 并使用新的图分区进行并行化训练. 在每次训练迭代结束时, 子图的实际运行时间将发送回图分区程序, 该程序通过最小化实际运行时间与预测运行时间之间的差异来更新成本模型. 实验表明这种基于线性回归的图分区方式的性能比现有的图分区策略高1.4倍.
5.6 存在挑战及相应优化技术
针对大规模图神经网络训练存在的挑战, 本节总结了多种优化技术, 并详细阐述了各典型系统的解决方案. 图9描述了挑战、优化技术、图神经网络系统三者之间的关联关系. 为扩展图传播过程所采用的以顶点为中心模型、以边为中心模型的图传播模型被很多系统使用, 为了阅读清晰, 图中不做连线标注. 并行计算方法、消息融合技术可以解决训练图神经网络计算、存储复杂度高的问题, 现有系统根据单机多卡或多机分布式的处理架构, 并结合所使用的图传播模型采用不同的图神经网络并行计算方法提高计算效率. 系统NeuGraph、DGL采用了消息融合技术来减少中间消息张量所带来的内存消耗, 降低了存储复杂度. 为应对频繁的消息传递带来的通信开销, 可以采用缓存技术, 系统AliGraph提出顶点重要性度量标准, 将重要顶点邻居进行缓存来减少计算节点之间的消息传递, 还可以采用局部感知划分, 将同一分区中的顶点之间的边尽可能得多, 从而减少通信开销. 为平衡计算负载, 许多系统采用了适合系统架构的图分区技术, 其中Roc采用线性回归图分区, 不仅将顶点和边的数量作为衡量因素, 还结合相关的硬件特征, 更适用于图神经网络的分布式训练. 在利用GPU加速训练时, NeuGraph的行列交替的调度方式与Roc采用代价模型来进行动态内存管理的方式都可减少GPU与主机的消息传递开销, 进而最小化数据移动, 提高系统性能.
06
实验总结
6.1 实验设置
本文对现有开源的图神经网络系统Euler、PyTorch Geometric、DGL以及AliGraph进行配置, 并从多个维度测试系统性能. 所有单机系统的实验都独立运行于相同实验环境中CPU: Intel(R) Core(TM) i7-7800X; 运行内存: 64 GB; GPU: NVIDIA Corporation Device GT 1080×2; 显存: 11 GB. 可扩展性实验运行于阿里云平台. 实验测试所采用的算法包括: 图卷积神经网络GCN、图注意力网络GAT、以及归纳式学习算法GraphSAGE. 本文的实验设置总结于表2.
实验使用的数据集包括: Cora、Citeseer、PubMed[58]3个引文网络数据集、Reddit社交网络数据集以及Web-Google数据集[59]. 这些数据集信息汇总于表3. 3个规模较小的引文网络数据集用于单机系统测试. 为了测试分布式系统的可扩展性, 本文采用Web-Google数据集, 并人工生成300维顶点标签用于训练.
6.2 测评指标
本文从多个方面对图神经网络系统进行了测试. 首先, 论文将图神经网络算法在原始论文中提供的精确度作为基线, 与测评系统的实验准确度进行比较, 以验证测评系统训练图神经网络模型的有效性. 这里的有效性是指系统训练后的算法模型能够在给定数据集的测试精度上与原论文基本保持一致. 第二, 论文对测评系统训练图神经网络模型的时间进行比较, 以证明系统的性能, 为了减少差异, 论文为每个实验记录了10次运行后的平均结果. 通过分析实验结果, 论文进一步验证了上述总结的优化技术的有效性. 第三, 为证明小批量训练方法对基于谱方法的GCN模型精度的影响, 论文采用小批量训练方法来分布式训练GCN模型, 将结果与全批量训练的精确度进行对比. 第四, 为测评系统的存储复杂度, 论文记录各系统训练图神经网络模型时的内存消耗. 第五, 论文针对分布式系统进行实验, 以验证其可扩展性. 大规模图神经网络的训练必须依靠分布式来实现, 而对于分布式系统来说, 能否在扩展性方面实现线性加速是衡量系统性能的重要指标.
6.3 结果与分析
(1)精度. 表3展示了DGL、PyTorch Geometric和Euler这3个系统在3个数据集Cora、PubMed、Citeseer[58]上训练图神经网络算法GCN、GAT、GraphSAG-mean的精确度, 将其与算法原始论文中的精度做对比, 通过结果可以发现在大多数情况下, 这些系统训练模型的精度偏差小于0.01, 实验结果验证了系统的有效性. 原始论文的图神经网络模型在现有数据流框架TensorFlow上进行训练, 采用的是传统的计算图模式. DGL与PyTorch Geometric采用的是消息传递模型, Euler采用的是以顶点为中心的消息传递模型, 这些处理模型都基于图神经网络的计算模式进行设计, 能够比现有数据流框架更好地表示算法中图传播的部分. 这种结合图传播的模型设计不仅为保证系统有效性提供了基础, 也为系统底层优化提供了机会.
(2)性能. 本文文首先对比了PyG-CPU, DGL-CPU, Euler这3个系统在GCN和GAT算法上的性能, 实验使用了Cora、Citeseer、PubMed[58]这3个数据集, 每个数据集运行200个epoch. 为了公平, 所有系统训练的数据数量大致相同. 实验结果如图10所示. DGL、Euler在较大图PubMed数据集中的性能明显优于PyG, 主要原因归功于DGL的消息融合技术, 在神经网络前向计算中通过将中间消息直接累和到目标顶点来避免生成消息张量. DGL为用户提供丰富的内建融合函数, 能够构建多种图神经网络模型, 消息的融合降低了内存访问频率, 带来了性能方面的优势. Euler系统所需的输入数据格式特殊, 处理过程复杂, 因此我们开发了一个数据处理框架来自动地将现有的数据集通过格式转换最终输入到系统中, 简化了操作流程. Euler的底层图引擎优化了图的存储结构: AliasTable和PartialSum, 将图算法中最高频的采样操作的时间复杂度降为O(1)和O(log(N)), 提高了在大规模数据集上的性能.
然后本文对比了PyG-GPU, DGL-GPU在GCN、GAT、GraphSAGE这3个算法上的性能, 在Cora、Citeseer、PubMed[58]数据集上分别运行200个epoch并记录运行时间. 实验结果如图11所示. 在GPU上, PyG的性能大多数情况下优于DGL, 这是由于PyG-GPU采用了图批量处理方法, 直接将大图按照连接断开的位置分解成多个子图. 系统自动生成新的子图的邻接矩阵, 在节点维度上合并特征矩阵, 来支持具有不同大小的多个图实例. 在断开连接的图之间不需要消息传递, 因此可以对具有不同大小的子图进行批量处理, 提高了系统性能. 并且PyG提供了系统内置图数据结构, 采用COO格式存储图结构信息, 以索引的方式可快速查找边上信息的流向, 按边关系直接生成中间消息, 这种方法提高了信息聚合速度, 与通过矩阵乘法实现方式相比, 更适用于图数据上的操作.
小批量并行训练方式对基于谱方法GCN模型精度的影响. 基于空间方法的图卷积网络使用的是小批量梯度下降方法, 这种方法可以直接用于分布式训练环境中. 而基于谱方法GCN的训练与其不同, 使用的是全批量梯度下降方法, 其中的图卷积运算需要利用图中顶点之间的交互来传播顶点的特征向量, 计算每个样本的梯度无法被分解, 所以无法在分布式环境中直接使用全批量梯度下降方法训练GCN. 目前大多数系统采用的分布式训练方法是: 对图中用于最终任务的顶点进行k阶邻居的采样, 再利用小批量梯度下降的方法训练每一个样本, 然后对部分梯度进行聚合. 本文对卷积图神经网络GCN进行实验, 在Euler系统上比较了模型在单机和分布式情况下运行200个epoch能够达到的准确度. 实验结果如图12所示, 采用小批量梯度下降的方法分布式训练GCN, 对节点邻居进行k阶邻居采样会损失部分节点邻域信息, 模型准确度在所有3个数据集上均低于单机情况下的效果.
(3)内存消耗. 表5比较了DGL、PyTorch Geometric和Euler这3个系统在4个数据集Cora、PubMed、Citeseer[58]、Reddit上训练图神经网络算法GCN、GAT的内存消耗. 为了保证对比公平, 所有系统训练的数据数量相同. 通过实验结果可以发现, DGL的消息融合技术不仅带来了速度优势, 还带来了内存方面的优势. 系统的存储复杂度正比于图中边的数量, 边的数量越多, 图神经网络训练产生的中间消息越多. 在稠密图Reddit上, PyTorch Geometric训练GCN模型的内存消耗是DGL的4.5倍, 并且在训练GAT模型时超出运行内存. Euler系统默认使用较小的batch_size参数, 虽然内存消耗小, 但其训练速度是DGL的24倍.
(4)可扩展性. 本文对现有分布式图神经网络系统AliGraph进行实验, 记录其在80万个顶点500万条边的Google数据集[59]上训练GCN模型一个epoch所需时间. 实验运行于阿里云平台(16个节点; CPU: Intel Xeon (Cascade Lake) Platinum 8269CY; 运行内存: 16 GB). AliGraph采用以顶点为中心的编程模型, 采用结构化存储和属性特定存储, 来存储大规模原始数据, 能够满足图神经网络模型对数据频繁访问的要求, 并对满足重要性度量的顶点邻居进行缓存, 减少了消息传递开销, 进一步提高了系统性能. 如图13所示, 实验证明随着机器数的增加, AliGraph能实现近似线性的加速比. 但是, 分布式情况下由于参数的聚合需要频繁的与参数服务器进行消息传递, 增加了通信开销, 并且缓存策略会引起冗余存储与计算开销, 其训练性能与单机训练相比改变并不明显. 单机多卡实验. 本文对系统DGL和PyTorch Geometric在单机多卡环境下进行实验以测试系统可扩展性. 实验运行于阿里云平台(GPU: NVIDIA P100×8; 显存: 16 GB; CPU内存: 480 GB). 实验采用Reddit数据集在算法GraphSAGE上进行测试, 对两个系统在不同GPU数量下训练30个epoch的时间进行记录. 如图14所示, DGL比PyG具有更好的性能, 但PyG拥有更好的可扩展性, 随着计算节点数量的增加性能提升更加显著.
07
总结
本文首先简要介绍了图神经网络的发展, 并对典型的图神经网络算法的计算模式进行了介绍, 并简要分析了图神经网络训练的难点. 然后本文对现有图神经网络系统做了详细描述, 并对这些系统从系统架构、处理模型以及优化策略和系统易用性等多个角度进行分析和总结, 总结了针对图神经网络系统的多种优化技术, 最后使用目前可用的开源系统验证了现有分布式图神经网络系统的有效性. 经过论文分析与总结, 发现现有图神经网络系统仍存在以下问题, 同时也是未来的研究方向: 首先, 目前系统所采用的架构仍依赖于现有数据流框架, 现有数据流框架针对深度神经网络的运算做了一系列优化, 但缺少针对图操作的优化尤其是高效分布式图操作, 与这些框架结合起来搭建系统, 制约了分布式图神经网络系统的进一步发展. 第二, 目前系统所采用的小批量并行计算方式, 并不适用于基于谱方法的图卷积网络, 本文通过实验发现, 采用这种并行计算方式会对基于谱方法图卷积网络的训练精度产生影响. 第三, 图的分区操作和通信管理是影响系统性能的关键因素, 尽管目前的系统已经在这两方面提出多种优化, 减少了内存消耗和通信开销, 但这两者仍存在非常大的优化空间.
参考文献
[1]Redmon J, Divvala S, Girshick R, Farhadi A. You only look once: Unified, real-time object detection. In: Proc. of the 2016 IEEE Conf. on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 779–788. [doi: 10.1109/CVPR.2016.91]
[2]Ren SQ, He KM, Girshick R, Sun J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149. [doi:10.1109/TPAMI.2016.2577031]
[3]Luong MT, Pham H, Manning CD. Effective approaches to attention-based neural machine translation. In: Proc. of the 2015 Conf. on Empirical Methods in Natural Language Processing. Lisbon: Association for Computational Linguistics, 2015. 1412–1421. [doi: 10.18653/v1/D15-1166]
[4]Wu YH, Schuster M, Chen ZF, et al. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv: 1609.08144, 2016.
[5]Hinton G, Deng L, Yu D, Dahl GE, Mohamed AR, Jaitly N, Senior A, Vanhoucke V, Nguyen P, Sainath TN, Kingsbury B. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine, 2012, 29(6): 82-97. [doi:10.1109/MSP.2012.2205597]
[6]Sanchez-Gonzalez A, Heess N, Springenberg JT, Merel J, Riedmiller M, Hadsell R, Battaglia P. Graph networks as learnable physics engines for inference and control. In: Proc. of the 35th Int’l Conf. on Machine Learning. Stockholm: PMLR, 2018. 4470–4479.
[7]Battaglia PW, Pascanu R, Lai M, Rezende DJ, Kavukcuoglu K. Interaction networks for learning about objects, relations and physics. In: Proc. of the 30th Int’l Conf. on Neural Information Processing Systems. Barcelona: NIPS, 2016. 4509–4517. [doi: 10.5555/3157382.3157601]
[8]Hamilton WL, Ying R, Leskovec J. Representation learning on graphs: Methods and applications. IEEE Data Engineering Bulletin, 2017, 40(1): 52-74.
[9]Brandes U, Gaertler M, Wagner D. Experiments on graph clustering algorithms. In: Proc. of the 11th European Symp. on Algorithms. Budapest: Springer, 2003. 568–579. [doi: 10.1007/978-3-540-39658-1_52]
[10]Fout A, Byrd J, Shariat B, Ben-Hur A. Protein interface prediction using graph convolutional networks. In: Proc. of the 31st Int’l Conf. on Neural Information Processing Systems. Long Beach: NIPS, 2017. 6533–6542. [doi: 10.5555/3295222.3295399]
[11]Jeong C, Jang S, Park E, Choi S. A context-aware citation recommendation model with BERT and graph convolutional networks. Scientometrics, 2020, 124(3): 1907-1922. [doi:10.1007/s11192-020-03561-y]
[12]Ribeiro LFR, Saverese PHP, Figueiredo DR. struc2vec: Learning node representations from structural identity. In: Proc. of the 23rd ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining. Halifax: ACM, 2017. 385–394. [doi: 10.1145/3097983.3098061]
[13]Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. In: Proc. of the 5th Int’l Conf. on Learning Representations. Toulon: OpenReview.net, 2017.
[14]Chen J, Ma TF, Xiao C. FastGCN: Fast learning with graph convolutional networks via importance sampling. In: Proc. of the 6th Int’l Conf. on Learning Representations. Vancouver: OpenReview.net, 2018.
[15]Huang X, Li JD, Hu X. Accelerated attributed network embedding. In: Proc. of the 2017 SIAM Int’l Conf. on Data Mining. Houston: SIAM, 2017. 633–641. [doi: 10.1137/1.9781611974973.71]
[16]Hamilton WL, Ying R, Leskovec J. Inductive representation learning on large graphs. In: Proc. of the 31st Int’l Conf. on Neural Information Processing Systems. Long Beach: NIPS, 2017. 1025–1035. [doi: 10.5555/3294771.3294869]
[17]Wang ZQ, Tan YW, Zhang M. Graph-based recommendation on social networks. In: Proc. of the 2010 12th Int’l Asia-Pacific Web Conf. Busan: IEEE, 2010. 116–122. [doi: 10.1109/APWeb.2010.60]
[18]Hamaguchi T, Oiwa H, Shimbo M, Matsumoto Y. Knowledge transfer for out-of-knowledge-base entities: A graph neural network approach. In: Proc. of the 26th Int’l Joint Conf. on Artificial Intelligence. Melbourne: IJCAI.org, 2017. 1802–1808. [doi: 10.24963/ijcai.2017/250]
[19]Liben-Nowell D, Kleinberg J. The link-prediction problem for social networks. Journal of the American Society for Information Science and Technology, 2007, 58(7): 1019-1031. [doi:10.1002/asi.20591]
[20]Abadi M, Barham P, Chen JM, et al. TensorFlow: A system for large-scale machine learning. In: Proc. of the 12th USENIX Conf. on Operating Systems Design and Implementation. Savannah: USENIX Association, 2016. 265–283. [doi: 10.5555/3026877.3026899]
[21]PyTorch.
[22]Chen TQ, Li M, Li YT, Lin M, Wang NY, Wang MJ, Xiao TJ, Xu B, Zhang CY, Zhang Z. MXNet: A flexible and efficient machine learning library for heterogeneous distributed systems. arXiv: 1512.01274, 2015.
[23]Yu D, Eversole A, Seltzer ML, Yao KS, Guenter B, Kuchaiev O, Seide F, Wang HM, Droppo J, Huang ZH, Zweig G, Rossbach CJ, Currey J. An introduction to computational networks and the computational network toolkit. In: Proc. of the 15th Annual Conf. of the Int’l Speech Communication Association. Singapore: ISCA, 2014.
[24]Chen R, Shi JX, Chen YZ, Zang BY, Guan HB, Chen HB. PowerLyra: Differentiated graph computation and partitioning on skewed graphs. ACM Trans. on Parallel Computing, 2018, 5(3): 13. [doi:10.1145/3298989]
[25]Gonzalez JE, Low Y, Gu HJ, Bickson D, Guestrin C. Powergraph: Distributed graph-parallel computation on natural graphs. In: Proc. of the 10th USENIX Symp. on Operating Systems Design and Implementation. Hollywood: USENIX Association, 2012. 17–30.
[26]Low Y, Bickson D, Gonzalez J, Guestrin C, Kyrola A, Hellerstein JM. Distributed graphlab: A framework for machine learning and data mining in the cloud. Proc. of the VLDB Endowment, 2012, 5(8): 716-727. [doi:10.14778/2212351.2212354]
[27]Malewicz G, Austern MH, Bik AJC, Dehnert JC, Horn I, Leiser N, Czajkowski GJ. Pregel: A system for large-scale graph processing. In: Proc. of the 2010 ACM SIGMOD Int’l Conf. on Management of Data. Indianapolis: ACM, 2010. 135–146. [doi: 10.1145/1807167.1807184]
[28]Xiao WC, Xue JL, Miao YS, Li Z, Chen C, Wu M, Li W, Zhou LD. Tux²: Distributed graph computation for machine learning. In: Proc. of the 14th USENIX Conf. on Networked Systems Design and Implementation. Boston: USENIX Association, 2017. 669–682. [doi: 10.5555/3154630.3154684]
[29]Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G. The graph neural network model. IEEE Trans. on Neural Networks, 2009, 20(1): 61-80. [doi:10.1109/TNN.2008.2005605]
[30]Gallicchio C, Micheli A. Graph echo state networks. In: Proc. of the 2010 Int’l Joint Conf. on Neural Networks. Barcelona: IEEE, 2010. 1–8. [doi: 10.1109/IJCNN.2010.5596796]
[31]LeCun Y, Bengio Y. Convolutional networks for images, speech, and time series. In: Arbib MA, ed. Handbook of Brain Theory and Neural Networks. Cambridge: MIT Press, 1995.
[32]LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444. [doi:10.1038/nature14539]
[33]Li RY, Wang S, Zhu FY, Huang JZ. Adaptive graph convolutional neural networks. In: Proc. 32nd AAAI Conf. on Artificial Intelligence, the 30th Innovative Applications of Artificial Intelligence, the 8th AAAI Symp. on Educational Advances in Artificial Intelligence. New Orleans: AAAI, 2018. 3546–3553.
[34]Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering. Proc. of the 30th Int’l Conf. on Neural Information Processing Systems. Barcelona: NIPS, 2016. 3844–3852. [doi: 10.5555/3157382.3157527]
[35]Levie R, Monti F, Bresson X, Bronstein MM. Cayleynets: Graph convolutional neural networks with complex rational spectral filters. IEEE Trans. on Signal Processing, 2019, 67(1): 97-109. [doi:10.1109/TSP.2018.2879624]
[36]Gilmer J, Schoenholz SS, Riley PF, Vinyals O, Dahl GE. Neural message passing for quantum chemistry. In: Proc. of the 34th Int’l Conf. on Machine Learning. Sydney: PMLR, 2017. 1263–1272.
[37]Velickovic P, Cucurull G, Casanova A, Romero A, Liò P, Bengio Y. Graph attention networks. arXiv: 1710.10903, 2017.
[38]Li YJ, Vinyals O, Dyer C, Pascanu R, Battaglia P. Learning deep generative models of graphs. arXiv: 1803.03324, 2018.
[39]You JX, Ying R, Ren X, Hamilton W, Leskovec J. GraphRNN: Generating realistic graphs with deep auto-regressive models. In: Proc. of the 35th Int’l Conf. on Machine Learning. Stockholm: PMLR, 2018. 5708–5717.
[40]Wu ZH, Pan SR, Long GD, Zhang CQ. Graph waveNet for deep spatial-temporal graph modeling. In: Proc. of the 28th Int’l Joint Conf. on Artificial Intelligence. Macao: IJCAI.org, 2019. 1907–1913. [DOI: 10.24963/ijcai.2019/264]
[41]Guo SN, Lin YF, Feng N, Song C, Wan HY. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In: Proc. of the 33rd AAAI Conf. on Artificial Intelligence, 31st Conf. on Innovative Applications of Artificial Intelligence, the 9th Symp. on Educational Advances in Artificial Intelligence. Honolulu: AAAI, 2019. 922–929. [doi: 10.1609/aaai.v33i01.3301922]
[42]Cai HY, Zheng VW, Chang KCC. A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Trans. on Knowledge and Data Engineering, 2018, 30(9): 1616-1637. [doi:10.1109/TKDE.2018.2807452]
[43]Cui P, Wang X, Pei J, Zhu WW. A survey on network embedding. IEEE Trans. on Knowledge and Data Engineering, 2019, 31(5): 833-852. [doi:10.1109/TKDE.2018.2849727]
[44]Goyal P, Ferrara E. Graph embedding techniques, applications, and performance: A survey. Knowledge-based Systems, 2018, 151: 78-94. [doi:10.1016/j.knosys.2018.03.022]
[45]Wu ZH, Pan SR, Chen FW, Long GD, Zhang CQ, Yu PS. A comprehensive survey on graph neural networks. IEEE Trans. on Neural Networks and Learning Systems, 2021, 32(1): 4-24. [doi:10.1109/TNNLS.2020.2978386]
[46]Zhou J, Cui GQ, Hu SD, Zhang ZY, Yang C, Liu ZY, Wang LF, Li CC, Sun MS. Graph neural networks: A review of methods and applications. arXiv: 1812.08434, 2018.
[47]Wang MJ, Yu LF, Zheng D, Gan Q, Gai Y, Ye ZH, Li MF, Zhou JJ, Huang Q, Ma C, Huang ZY, Guo QP, Zhang H, Lin HB, Zhao JB, Li JY, Smola A, Zhang Z. Deep graph library: Towards efficient and scalable deep learning on graphs. arXiv: 1909.01315, 2019.
[48]Fey M, Lenssen JE. Fast graph representation learning with PyTorch Geometric. arXiv: 1903.02428, 2019.
[49]Ma LX, Yang Z, Miao YS, Xue JL, Wu M, Zhou LD, Dai YF. Neugraph: Parallel deep neural network computation on large graphs. In: Proc. of the 2019 USENIX Annual Technical Conf. Renton: USENIX Association, 2019. 443–458.
[50]Liang SW, Wang Y, Liu C, He L, Li HW, Xu DW, Li XW. EnGN: A high-throughput and energy-efficient accelerator for large graph neural networks. IEEE Trans. on Computers, 2020. [doi:10.1109/TC.2020.3014632]
[51]A graph system developed by Alibaba.
[52]Jiang JW, Xiao P, Yu LL,Cheng JF大规模c程序设计 pdf, Miao XP, Zhang ZP, Cui B. PSGraph: How Tencent trains extremely large-scale graphs with Spark? In: Proc. of the 2020 IEEE 36th Int’l Conf. on Data Engineering. Dallas: IEEE, 2020. 1549–1557. [doi: 10.1109/ICDE48307.2020.00137]
[53]Zhu R, Zhao K, Yang HX, Lin W, Zhou C, Ai BL, Li Y, Zhou JG. Aligraph: A comprehensive graph neural network platform. Proc. of the VLDB Endowment, 2019, 12(12): 2094-2105. [doi:10.14778/3352063.3352127]
[54]Jia ZH, Lin SN, Gao MY, Zaharia M, Aiken A. Improving the accuracy, scalability, and performance of graph neural networks with roc. In: Proc. of the Machine Learning and Systems. Austin: MLSys, 2020. 187–198.
[55]Zhang DL, Huang X, Liu ZQ, Hu ZY, Song XZ, Ge ZB, Zhang ZQ, Wang L, Zhou J, Shuang Y, Qi Y. AGL: A scalable system for industrial-purpose graph machine learning. arXiv: 2003.02454, 2020.
[56]
[57]Zhou J, Li XL, Zhao PL, Chen CC, Li LF, Yang XX, Cui Q, Yu J, Chen X, Ding Y, Qi YA. Kunpeng: Parameter server based distributed learning systems and its applications in alibaba and ant financial. In: Proc. of the 23rd ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining. Halifax: ACM, 2017. 1693–1702. [doi: 10.1145/3097983.3098029]
[58]Sen P, Namata G, Bilgic M, Getoor L, Galligher B, Eliassi-Rad T. Collective classification in network data. AI Magazine, 2008, 29(3): 93. [doi:10.1609/aimag.v29i3.2157]
[59]









