在图象处理的过程中,消除图象的噪音干扰是一个十分重要的问题。本文借助matlab软件,采用空域混频的方法,对图象进行平滑和白平衡处理。平滑空间滤波器用于模糊处理和减少噪音,经常在图象的预处理中使用;锐化空间滤波器主要用于突出图象中的细节或则提高被模糊了的细节。本文使用的平滑滤波器有中值滤波器和高斯低通滤波器,其中,中值滤波器对清除酱汁噪音非常有效,高斯低通滤波器对清除高斯噪音疗效比较好。使用的散景滤波器有反散景掩膜混频、Sobel边沿检查、Laplacian边沿检查以及Canny算子边沿检查滤波器。不同的混频形式,在特定的图象处理应用中有着不同的疗效和各自的优势。2,模板大小分别是3x35x53*3中值滤波器模板,7x7;利用固定残差sigma=1.5形成高斯滤波器.附件有形成高斯滤波器的方式。空域混频是直接对图象的数据做空间变换达到混频的目的。它是一种邻域运算,其机理就是在待处理的图象中逐点地联通模板,滤波器在该点地响应通过事先定义的滤波器系数与混频模板扫过区域的相应象素值的关系来估算。如果输出象素是输入象素邻域象素的线性组合则称为线性混频(例如最常见的均值混频和高斯滤波),否则为非线性滤波(中值滤波、边缘保持混频等)。
空域滤波器从处理疗效上可以平滑空间滤波器和锐化空间滤波器:平滑空间滤波器用于模糊处理和减少噪音,经常在图象的预处理中使用;锐化空间滤波器主要用于突出图象中的细节或则提高被模糊了的细节。模板在源图像中联通的过程中,当模板的一条边与图象轮廓重合后,模板中心继续向图象边沿紧靠,那么模板的某一行或列都会处于图象平面之外,此时最简单的方式就是将模板中心点的联通范围限制在距离图象边沿不大于(n-1)/2个象素处,单处理后的图象比原始图象稍小。如果要处理整幅图象,可以在图象轮廓边沿时用全部包含于图象中的模板部份来混频所有图象,或者在图象边沿以外再补上一行和中学值滤波器是一种非线性统计滤波器,它的响应基于图象滤波器包围的图象区域中象素的排序,然后由统计排序的中间值替代中心象素的值。它比小规格的线性平滑滤波器的模糊程度显著要低,对处理脉冲噪音(椒盐噪音)非常有效。中值滤波器的主要功能是使拥有不同灰度的点看起来更接近于它的毗邻值,去除这些相对于其邻域象素更亮或更暗,并且其区域大于滤波器区域一半的孤立象素集。在一维的情况下,中值滤波器是一个富含质数个象素的窗口。在处理过后,位于窗口正中的象素的灰度值,用窗口内各象素灰度值的中值取代。
例倘若窗口宽度为5,窗口中象素的灰度值为80、90、200、110、120,则中值为110,因为按小到大(或大到小)排序后,第三位的值是110。于是原理的窗口正中的灰度值200就由110代替。如果200个噪音的尖峰,则将被滤除。然而,如果它是一个讯号,则混频后就被清除,降低了帧率。因此中值滤波在个别情况下抑制噪音,而在另一些情况下却会抑制讯号。将中值滤波推广到二维的情况。二维窗口的方式可以是正方形、近似方形的或十字形等。本次作业使用正方形模板进行混频,它的中心通常坐落被处理点上。窗口的大小对混频疗效影响较大。根据上述算法借助MATLAB软件编程,对源图像test1和test2进行混频处理,结果如下图:可见,窗口的大小对混频疗效影响较大。窗口越大,平滑疗效越显著,图像细节越模糊。高斯滤波是一种按照高斯函数的形状来选择模板残差的线性平滑混频方式。高斯平滑滤波器对清除服从正态分布的噪音是很有疗效的。一维零均值高斯函数为。其中,高斯分布参数决定了高斯滤波器的长度。对图象来说,常用二维零均值离散高斯函数作平滑滤波器,函数表达式如下:高斯函数具有5个重要性质:(来自:(1)二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的。
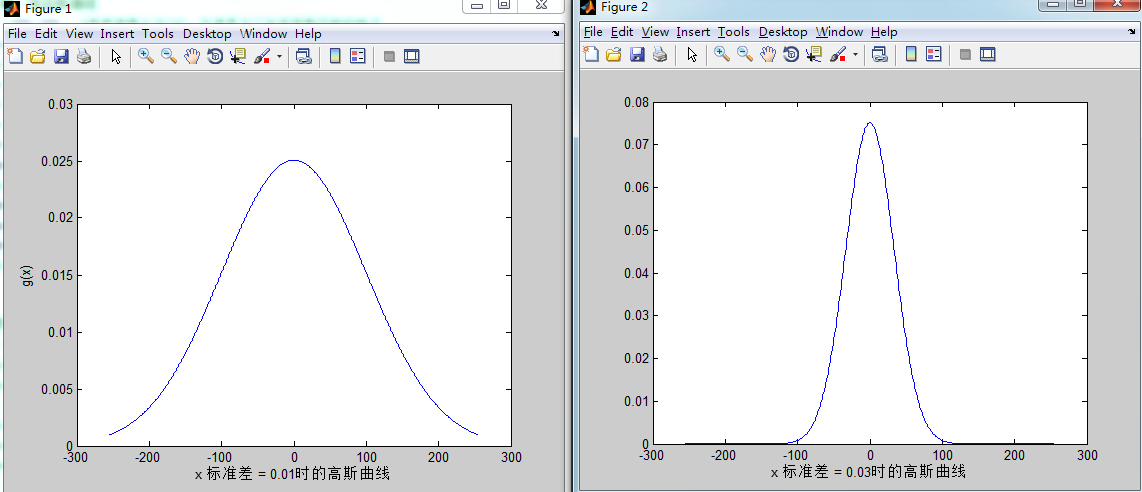
一般来说一幅图象的边沿方向是不知道的。因此,在混频之前是难以确定一个方向比另一个方向上要更多的平滑的。旋转对称性意味着高斯滤波器在后续的图象处理中不会偏向任一方向。本次作业学习了空域滤波器的使用,并且学习了怎样形成高斯函数。通过对实验结果的剖析可以发觉高斯函数对于细小的噪音优化疗效较好,而中值滤波对于大噪音也有一定的优化疗效。而前面的边沿提取作业,很明显的可以看出使用Canny算子的图片处理疗效要好好多,虽然仍然存在边沿不连续的问题,但是整体的边沿早已提取了下来。一、空域低通滤波器:分别用高斯滤波器和中值滤波器去平滑测试图象test1和2,模板大小分别是3x35x5,7x7;(利用固定残差sigma=1.5一个数值集合的中值n是这样的数值,即数值集合中有一还有一半小于或等于n。为了对一幅图象上的某点进行中值混频处理,首先将领域内的象素分类排序,确定其中值,并将中值赋于混频后图象中的相应象素点。这样,中值滤波器的主要公式是使拥有不同灰度的点看起来更接近于它的相邻点。事实上,我们使用mxm中值滤波器来消除这些相对于其领域象素更亮或更暗而且其区域大于/2(滤波区域的一半)的鼓励象素族。在这些情况下,“去除”的意思是强制为领域的中值灰度。
较大的族所遭到的影响显著较小。结果观察:通过运行结果可以看出从处理后的图象看,图像的平滑疗效较为显著,且受窗口的影响,窗口越大,平滑疗效越显著,图像细节越模糊,尤其是test2中人脸图象的耳朵部份,随着滤波器模板的减小,可以显著的感受到图象模糊的疗效。这三个模板中,感觉5x5的模板混频疗效最好。(1)二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的。一般来说,一幅图象的边沿方向是事先不知道的,因此,在混频前是难以确定一个方向上比另一方向上须要更多的平滑.旋转对称性意味着高斯平滑滤波器在后续边沿检查中不会偏向任一方向。(2)高斯函数是单值函数。这表明,高斯滤波器用象素邻域的加权均值来取代该点的象素值,而每一邻域象素点残差是随该点与中心点的距离单调增减的。这一性质是很重要的,因为边沿是一种图象局部特点,如果平滑运算对离算子中心很远的象素点一直有很大作用,则平滑运算会使图象失(3)高斯函数的付立叶变换频谱是重瓣的。正如下边所示,这一性质是高斯函数付立叶变换等于高斯函数本身这一事实的直接结论.图像常被不希望的高频讯号所污染(噪声和细纹理)。而所希望的图象特点(如边沿)高频份量。
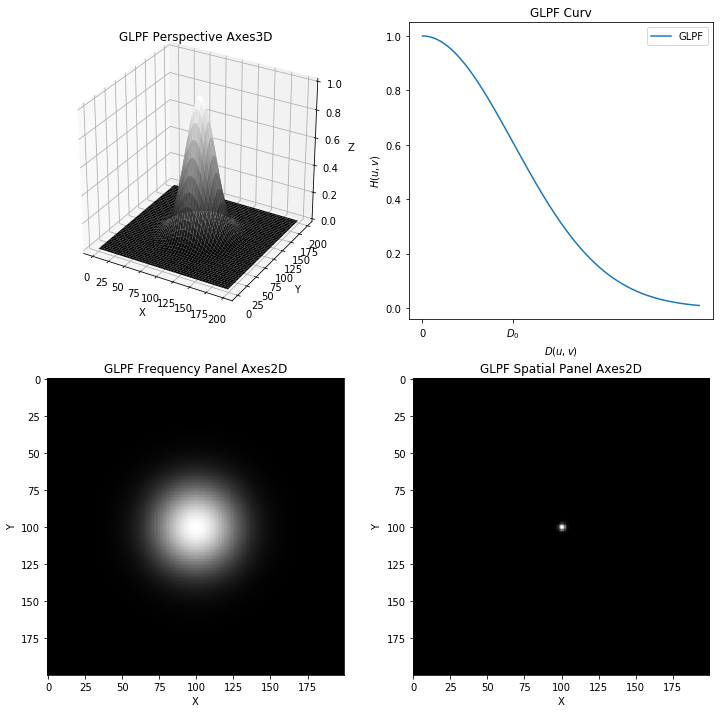
高斯函数付立叶变换的单叶意味着平滑图象不会被不需要的高频信号所污染,同时保留了大部分所需信表征的,而且和平滑程度的关系是十分简单的。σ越大,高斯滤波器的频带就越宽,平滑程度就越好。通过调节平滑程度参数σ,可在图象特点过于模糊(过平滑)与平滑图象中因为噪音和细纹理所造成的过多的不希望突变量(欠平滑)之间取得折衷。(5)由于高斯函数的可分离性,大高斯滤波器可以得以有效地实现.二维高斯函数卷积可以分两步来进行,首先将图象与一维高斯函数进行频域,然后将频域结果与方向垂直的相同一维高斯函数频域。因此,二维高斯滤波的估算量随混频模板厚度成线性下降而不是成平方下降。((int)(3.0sigma));opencv和sift 码也是如此做的,当然实际中可以虽然没有那么严格。我们可以使用 matlab 中的函数直接估算出高斯核,例如 3x3 高斯模板:filter=fspecial('gaussian',3,1);其中 sigma=1; sigma的取值决定了高斯函数窗口的大小。在实际中常常 看到 sigma 取值 0.8 或者正常情况下我们由高斯函数估算得 到的模板是浮点型数3*3中值滤波器模板,即double,但是有些情况我们为了加 快估算须要将模板处理成整数,对于常见的3x3 或者5x5 在图象预处理中,对图象进行平滑,去除噪音,恢复原始图象是一个重要内容。
本文设计了一个平滑尺度和模 板大小均可以改变的高斯滤波器,用它对多幅加入各类噪音 后的图象进行平滑,经过对各个结果图象的对比可知高斯滤波对服从正态分布的噪音消除疗效比较好,并且相比各个不 同参数,在平滑尺度为2,模板大小为7 时疗效最佳。 关键词图象预处理;平滑处理;平滑尺度;模板大小; 高斯滤波 一幅原始图象在获取和传输过程中会遭到各类噪音的干扰,使图象质量下滑,对剖析图象不利。反映到图象画面上, 主要有两种典型的噪音。一种是幅值基本相同,但出现的位 置随机的酱汁噪音,另一种则每一点都存在,但幅值随机分 布的随机噪音。为了抑制噪音、改善图象质量,要对图象进 行平滑处理。图像平滑处理的方式多种多样,有邻域平均、 中值滤波,高斯滤波、灰度最小残差的均值混频等。这里主 要就是剖析高斯滤波器的平滑疗效。以下即为本课题研究的 主要内容及要求: 第三,程序中实现不同平滑尺度、不同模板大小的高斯模板设计,并将设计结果显示下来; 第四,以Lena图象为例,进行加噪音,分析平滑的实验 效果。 高斯平滑滤波器的原理10 高斯滤波器是按照高斯函数的形状来选择残差的线性平滑滤波器。高斯平滑滤波器对清除服从正态分布的噪音是很 有疗效的。
一维零均值高斯函数为 。其中,高斯分布参数 定了高斯滤波器的长度。对图象来说,常用二维零均值离散高斯函数作平滑滤波器,函数表达式如下: 高斯函数具有5个重要性质: (1)二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的。一般来说一幅图象的边沿方向是 不知道的。因此,在混频之前是难以确定一个方向比另一个 方向上要更多的平滑的。旋转对称性意味着高斯滤波器在后 续的图象处理中不会偏向任一方向。 (2)高斯函数是单值函数。这表明,高斯滤波器用象素邻域的加权均值来取代该点的象素值,而每一邻域象素点的 权值是随着该点与中心点距离单调递减的。这一性质是很重 要的,因为边沿是一种图象局部特点。如果平滑运算对离算 子中心很远的象素点一直有很大的作用,则平滑运算会使图









