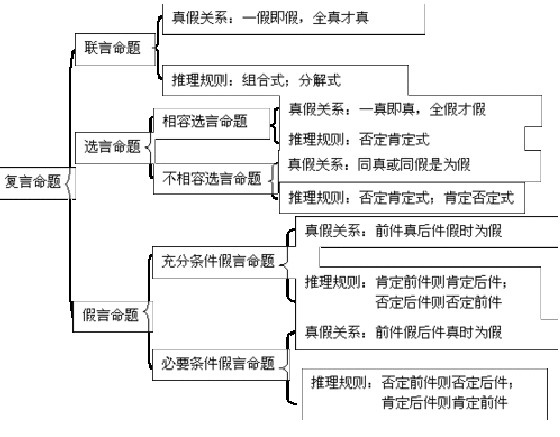
数理逻辑 主讲:邱晓红,2,数理逻辑简介,数理逻辑是用数学方法研究形式逻辑的科学。数学方法即符号方法,故数理逻辑又称符号逻辑。包含命题逻辑、谓词逻辑、证明论、模型论、递归函数、公理化集合论、归纳逻辑、模态逻辑、多值逻辑和时态逻辑等内容,与计算机有密切关系。,3,各知识点关联图,4,第一部分:数理逻辑,第一章 命题逻辑 1.1 命题及其表示 1.2 逻辑联结词 1.3 命题公式与解释 1.4 真值表与等价公式 1.5 命题公式的分类与蕴含式 1.6 其它逻辑联结词和最小功能完备联结词组 1.7 对偶与范式 1.8 推理理论 习 题 一 实验一 真值表的程序计算 第2章 谓词逻辑 2.1谓词的基本概念 2.2谓词公式与解释 2.3变元的约束,2.4谓词演算的等价式与蕴含式 2.5谓词公式范式 2.6 谓词演算的推理理论 习 题 二 实验二 命题逻辑简单推理系统 第3章 基于归结原理的推理证明* 3.1谓词公式与子句集 3.2 海伯伦(HERBRAND)理论 3.3 归结原理(RESOLUTION METHOD) 3.4 归结过程的控制策略 习 题 三 实验三 归结原理的程序实现,5,第一章:命题逻辑,主要内容:命题及表示、联结词、命题公式与翻译、真值表与等价公式、重言式与蕴涵式、其他联结词、对偶与范式、推理理论。
教学要求:深刻理解和掌握命题逻辑中的基本概念和基本方法。 重点:命题逻辑中的基本概念和基本推理方法 难点:推理理论。 实践活动:真值表的程序计算,6,1.1 命题及其表示,定义1.1.1 能够判断真假的陈述句称为命题(Proposition)。命题的判断结果称为命题的真值,常用T(True)(或1)表示真,F(False)(或0)表示假。真值为真的命题称为真命题,真值为假的命题称为假命题。 判定一个句子是否为命题要分为两步:一是判定是否为陈述句,二是能否判定真假,二者缺一不可。,7,8,解 在上述的十个句子中,(2)、(9)为祈使句,(4)为疑问句,(5)、(6)虽然是陈述句,但(5)没有确定的真值,其真假随x、y取值的不同而有改变,(6)是悖论(Paradox)(即由真能推出假,由假也能推出真),因而(2)、(4)、(5)、(6)、(9)均不是命题。(1)、(3)、(7)、(8)、(10)都是命题,其中(10)虽然现在无法判断真假,但随着科技的进步是可以判定真假的。需要进一步指出的是,命题的真假只要求它有就可以,而不要求立即给出。如例1.1.1的(8)1+101=110,它的真假意义通常和上下文有关,当作为二进制的加法时,它是真命题,否则为假命题,9,命题分类命题标识符,根据命题的结构形式,命题分为原子命题和复合命题。
定义1.1.2 不能被分解为更简单的陈述语句的命题称为原子命题(Simple Proposition )。由两个或两个以上原子命题组合而成的命题称为复合命题(Compound Proposition )。 定义1.1.3 表示原子命题的符号称为命题标识符(Identifier)。 命题标识符依据表示命题的情况,分为命题常元和命题变元。,10,1.2 逻辑联结词,一个复合命题,不论其构成多么复杂,一般都可以分析出构成该命题的原子命题。下面介绍5种常用的逻辑联结词(Logical Connectives ),分别是“非”(否定联结词)、“与”(合取联结词)、“或”(析取联结词)、“若则”(条件联结词)、“当且仅当”(双条件联结词),通过这些联结词可以把多个原子命题复合成一个复合命题。,11,1.2.1否定联结词,12,1.2.2合取联结词,13,1.2.3析取联结词,14,1.2.4条件联结词,15,1.2.5 双条件联结词,16,1.2.6字位运算与布尔检索,17,18,1.3 命题公式与解释,上一节介绍了5种常用的逻辑联结词,利用这些逻辑联结词可将具体的命题表示成符号化的形式。对于较为复杂的命题,需要由这5种逻辑联结词经过各种相互组合以得到其符号化的形式,那么怎样的组合形式才是正确的、符合逻辑的表示形式呢?,19,1.3.1命题公式,20,1.3.2命题的符号化,21,命题的符号化范例,22,1.4 真值表与等价公式,23,真值表,24,真值表范例,25,26,1.4.2等价公式,27,28,1.4.2.1真值表法,29,12组常用的等价公式,30,1.4.2.2等值演算法,31,32,33,34,35,36,37,1.5 命题公式的分类与蕴含式,38,39,40,1.5.3蕴含式,41,42,1.5.3.1真值表法,43,1.5.3.2等值演算法,44,1.5.3.3分析法,45,1.6 其它逻辑联结词和最小功能完备联结词组,46,47,1.6.1.2 与非联结词(Nand)(),48,1.6.1.3 或非联结词(Nor)(),49,50,1.6.2最小功能完备联结词组,51,1.6.3联结词的逻辑电路表示,52,53,54,1.7 对偶与范式,55,1.7.1.2 对偶原理(Duality Principle),56,57,1.7.2命题公式的范式,58,59,1.7.2.2 析取范式与合取范式,60,求公式范式的步骤,61,62,1.7.2.3 范式的应用,63,1.7.3命题公式的主析取范式和主合取范式,64,65,66,67,68,(2)等值演算法,69,70,71,72,73,74,(2)等值演算法,75,76,1.7.3.3 主析取范式和主合取范式关系,77,78,79,1.7.3.4 主范式的应用,80,( 2) 命题公式类型的判定,81,82,(3) 解决实际问题,83,1.8 推理理论,84,85,1.8.1直接证法,86,87,88,89,90,1.8.2间接证法,91,1.8.2.2归谬法,92,习题课,提示:,提示:,提示:,解,答案:,解答,解,证明,116,117,实验一 真值表的程序计算,118,119,第二章:谓词逻辑,主要内容:谓词的概念与表示、命题函数与量词、谓词公式与翻译、变量的约束、谓词演算的等价式与蕴涵式、前束范式、谓词演算的推理理论。
教学要求:深刻理解和掌握谓词逻辑的基本概念和基本推理方法。 重点:谓词逻辑中的基本概念和基本推理方法 难点:谓词演算的推理理论 。 实践活动:命题逻辑简单推理系统,120,121,2.1谓词的基本概念,122,123,124,125,2.1.2量词,126,127,2.2谓词公式与解释,128,2.2.2谓词公式的解释,129,130,2.3变元的约束,131,132,133,2.3.2换名规则,134,135,2.3.3代替规则,136,2.4谓词演算的等价式与蕴含式,137,138,139,2.4.2谓词公式的分类,140,141,142,143,2.4.3谓词演算的等价式,144,2.4.3.1 量词的消去,145,146,2.4.3.2 量词与“”之间的关系,147,2.4.3.3 量词作用域的扩张与收缩,148,149,2.4.3.4 量词与命题联结词之间的一些等价式,150,2.4.4谓词演算的蕴含式,151,152,153,2.5谓词公式范式,154,155,156,157,158,2.5.2斯柯林范式,159,2.6 谓词演算的推理理论,160,2.6.1规则(全称指定规则)(Universal Specification),161,2.6.2(全称推广规则)(Universal Generalization),162,2.6.3(存在指定规则)(Existential Specification),163,2.6.4(存在推广规则)(Existential Generalization),164,165,166,167,168,习题课,解,解,解,证明:,183,实验二 命题逻辑简单推理系统,184,185,186,187,188,第三章:基于归结原理的推理证明,主要内容:谓词公式与子句集的概念,斯柯林(Skolem)标准范式及其求取过程,海伯伦(Herbrand)理论的H域及其解释,置换与合一,命题和谓词归结原理,归结过程的控制策略。
教学要求:深刻理解和掌握归结原理的基本概念和基本归结过程。 重点:归结原理的基本概念和基本归结方法 难点:归结原理的实现方法 。 实践活动:归结原理的程序实现,189,第3章 基于归结原理的推理证明*,190,3.1谓词公式与子句集,191,3.1.1.2 斯柯林(Skolem)标准范式,192,193,194,195,3.1.2子句与子句集,196,3.1.3不可满足意义下的一致性,197,3.1.4 PP1P2Pn的子句集,198,3.2 海伯伦(Herbrand)理论,199,200,3.2.2原子集,201,3.2.3 H域上的解释,202,203,3.3 归结原理(Resolution Method),204,3.3.1.2 置换的合成,205,3.3.1.3置换结合律,206,3.3.1.5最一般合一置换的求取算法,207,3.3.2命题逻辑中的归结原理,208,3.3.2.2归结推理过程,209,3.3.3一阶谓词逻辑中的归结原理,210,211,212,213,3.3.4归结原理的完备性,214,3.3.5利用归结原理进行定理证明,215,216,3.3.6应用归结原理进行问题求解,217,218,219,220,3.4 归结过程的控制策略,221,(2)控制策略的分类,222,3.4.2归结控制策略及其应用举例,223,224,225,226,实验三 归结原理的程序实现,227,