图一是自然科学家们使用的两个模型。以左边的地球运行轨道模型为例,我们很容易能认识到,它是个经过简化的真实世界。简化有两类,一类是直接忽略现实中的某些方面。比如这个轨道模型就省略了地球和太阳之间的水星和金星。另一类简化是对现实世界的扭曲(distortion)。譬如这个模型里的太阳就被缩小了很多倍;相对于地球和月亮,真实的太阳要大得多。太阳和地球之间的距离¾相对于地球的半径来说¾也被缩小了很多。这个模型虽然被简化得不真实了,却很有用:我们如果借助于它来解释地球上日食和月食的成因(讲解特定的理论),就特别容易让别人理解。
▲ 图一:模型两例
与此类似,右边的脱氧核糖核酸(DNA)模型也做了简化,例如每个碱基(两条螺旋链之间互补配对的部分)的分子结构都比模型中显示的复杂得多。我们虽然没有亲眼见过DNA,也能猜出它的每一部分之间不会有那么明显的颜色对比,模型设计者扭曲了颜色以便让我们更能看清DNA的结构。这两个例子告诉我们,科学研究人员做的模型,目的不是求真实,而是求有用、能帮助他们展示和表述理论。
经济学家用的模型也是一样的。我们也做简化:有的模型直接忽略了政府的存在;有的假设这世界上只有两个国家、两种产品。不同的是,我们经济学家不经常使用实物模型,而是用图形和数学方程式。也就是说,除了简化,我们还做了抽象化,譬如用曲线上每一点的高度代表消费者的支付意愿、用函数关系代表企业的生产技术约束、等等。从这个角度来说,经济学家使用的模型特别像是地图(Krugman, 1994)。地图也做简化,譬如交通图会忽略地面的建筑、地铁路线图会把弯道拉直;地图也做抽象化的处理,有宽度的街道变成了一条细线、奇形怪状的城市变成了一个圆点等等。地图不真实,但是我们都知道它有用。有意思的是,正是地图的不真实,让它变得更有用:想找行车路线的人,会上网查谷歌地图,很少有人去查更真实的谷歌卫星照片。经济学家用的模型也是一样的,不求真实、只为有用。
由此说来,经济学模型当然是在理论化的工作中起的作用最大。在近几十年的经济学发展过程中,主流经济学理论的展示几乎全是通过模型推导来实现的。模型也就占据了每个理论最核心的逻辑推理部分。
那么实证经济学研究为什么能用到模型呢?一则是因为有一部分实证研究的目的是要检验理论,需要表述理论,而此时使用模型推导经常会使表述更方便、清晰、严谨。应用一类的实证工作因为要用到现存的理论,而现存的理论多是围绕模型写成的,当然也会用到模型来表述理论。
这么说来记录一类的工作就用不到模型了?也能用到。这跟经济学领域的一个传统有关。在自然科学领域,可能因为发展时间长而使得分工更细,即使是针对同一个自然现象,记录、理论化、理论验证的工作也完全可以由不同的研究团队来完成。而在经济学领域则不然,单纯的记录性的工作不太容易被发表,研究人员往往要同时做一些理论化的工作来解释记录的现象,才能被认为是重要的贡献。以Eeckhout (2004) 为例,他用大量的人口普查数据来说明,美国城市人口规模服从Zipf分布的说法只适用于大城市,如果把小地方也包括进来,则服从对数正态分布。对数正态分布的一端和Zipf分布非常接近,光看大城市时不易区分。按说这个作为记录性的工作已经不错了,但是他在文章里继续往下做,写了一个模型,给对数正态分布的出现做一个理论解释。这样的例子有很多,即经济学者时常把记录性的工作和理论化的工作合并,就导致记录性的实证研究里也常常出现理论模型。
总结来说,经济学家和其他科学领域的研究人员一样,要做描述现象、验证理论和应用理论一类的实证研究。在这几类研究中都会涉及理论,而大部分理论是用模型推导的形式表述的,就导致实证经济学研究里会常常用到理论模型。
03. 以模型为依托的实证研究的比重
我们来做个简单的统计,看看近年来最重要的城市和区域经济学研究中有多少是实证研究,其中又有多少用到了理论模型。图二对经济学五大顶级期刊在2001-2018年间发表的城市和区域经济学领域的论文做了分类。五大期刊当然不具有代表性,但是完全有理由认为,这些论文是本领域最具影响力的研究成果。
从图中可以看出,纯理论的研究相对很少,只占7%;绝大多数的论文属于实证研究。这个倒也不难理解。经济学近三十年来较少有理论突破,既没有重大的范式改变(譬如引入理性预期的假设),也没有新的逻辑语言的引入(譬如博弈论语言的应用),更没有重大的理论创新。而这期间信息技术的飞速发展使数据的来源增多了,计算成本降低了,极大地促进了实证研究的发展。这个趋势贯穿于经济学的各个分支(Hamermesh, 2013)。
▲ 图二:以模型为依托的实证研究的比重,2001-2018
我把实证研究按照与模型的关系细分成几类。一类是没有任何模型的实证分析,这一类的文章占到总数的31%。这类研究并非不涉及理论。正如上面提到的,几乎每一种实证研究都离不开理论。这些研究没用到模型,只是因为其中的理论相对简单,几句话就可以说清楚,没必要做数学推演。以Baum-Snow (2007)为例,他想看美国高速公路系统的建立是不是推动了城市人口向郊区的转移。这个问题的逻辑一目了然,难点在于如何解决内生性的问题,就不需要用模型。再比如,Hodler和Raschky (2014)用全球的卫星灯光数据度量经济发展,看各国领导人的家乡是不是经济更加繁荣。这个问题的逻辑也不难理解,也就没有必要用模型。我前面说到国内的学者做实证研究时一般不用理论模型,就是说他们的研究大都属于这一类,问题的逻辑相对简单明了,不需要借助模型来表述。
其余超过全部研究60%的论文都用到了模型。这里面又大致可以分为三类:一类只是用模型说明道理,回归分析中估计的并不是模型的参数,我们把这一类研究叫做“以模型为依托的、非结构性的回归分析”;第二类不光用模型说明道理,而且所做的回归分析的目的就是为了估计模型的参数,我们把这一类研究叫做“以模型为依托的、结构性的回归分析”;最后一类应用的模型特别复杂,以至于模型的参数之多已经很难一次全部估计出来,不得不从他人的研究中借用一些参数的估值来进行反事实的分析,我们把这一类研究叫做“以模型为依托的、结构性的校准分析”。
我们下面就根据这个分类一一具体讨论模型在每一类实证研究中的应用。

04. 模型在非结构性实证研究中的作用
先来澄清几个概念。上面已经提到,结构性实证研究的目标就是要获得理论模型的参数,以便用模型来估算政策的效果或事件的影响。那么不是以获取模型参数为目标的研究,我们就称之为非结构性的研究。与结构性回归分析相对应,经济学家常常提到简化型的回归(reduced-form regression)。早期的理论经济学模型经常是一组(线性)方程,每个方程是一些内生和外生变量之间的关系,方程里的系数被称为结构性参数。直接用回归分析估计这组方程里的系数,就是结构性回归分析。另外一种常见的做法,是对方程组求解,把每一个内生变量表达成一组外生变量的函数,而根据这些函数用内生变量对外生变量做回归分析,就是简化型的回归分析。用简化型回归分析估计出来的系数一般来说不是模型的参数,而是模型参数的函数。近些年来,简化型回归分析这个概念有了更广义的用法,对一切从模型推演出来的或根据理论直觉写下的变量关系所做的回归分析,只要不是以获取模型的参数为目标,都可以叫做简化型回归分析。从下面的讨论中可以看到,我这里用的非结构性研究的概念,比广义上的简化型回归分析涵盖的种类还要多,包括用回归方法寻找断点、探究新建的指数与哪些变量相关等实证工作。
按照Holmes (2010)的说法,我们又可以把非结构性的研究细分为两类。一类是描述性的研究,只是给出不同变量之间的相关性,而不太注重因果关系的识别。早期的实证研究大多属于这一类。另外一类是基于实验方法(experimentalist approach)的研究,就是通过“自然实验”或是“可控实验”,来识别一个变量对另一个变量的因果效应(causal effect),其目标也是要估算政策的效果或事件的影响。我在这一节虽然把Holmes所说的两类非结构性研究合并在一起来讲,但也会偶尔提及这个分类。
▷ 模型能帮助澄清实证研究的目的和意义
随着信息技术的发展,数据越来越多,数据里的变量也越来越多,可供考察的变量之间的关系更是呈几何级数增长。那么我们做实证研究为什么要去看某个特定的变量之间的关系呢?这是每一篇报告实证研究结果的论文都需要讲清楚的问题,而借助于一个简单的模型常常是把这个问题讲清楚的最有效的方式。
最常见的例子是用模型阐明一个理论、导出两个变量之间是正相关或负相关,然后用回归分析验证这个关系。譬如Storeygard (2016)用模型说明,运输成本升高对远离经济中心的城市有更大的负面影响,他用非洲的数据检验这个推断。Lee和Lin (2018)用模型导出三个不同的变量关系,例如其中之一是说自然条件优越的街区更容易成为高收入的街区并能长期保持这种地位,他们用跨时一个多世纪(1880-2010)的美国人口普查数据来验证这些变量关系。一般来说,这类实证研究探索的是较深层次的变量之间的关系,这些关系背后的逻辑不是三言两语就能说清楚的,所以才有利用模型来表述的必要。
另有一些实证研究检验更加复杂一些的理论推断,比如说,涉及数量关系中斜率的变化或断点的存在。譬如Glaeser和Gyourko (2005)的文章指出,房产的寿命很长,因而一个城市的房产需求在萎缩和增加时,对城市的影响是不对称的。当需求萎缩时,房产并不会马上消失、供给是刚性的,因而房价会大幅下跌而城市人口只是缓慢地减少;而当需求增长时,只要房价高于建设成本就会有新房上市、供给是有弹性的,因而房价会缓慢上涨而人口会迅速增加。Glaeser和Gyourko (2005)用一个简单的模型推导出增长的城市和衰落的城市的各种不同表现,并用美国的数据对结果进行一一验证,为我们了解衰落的城市提供了一个新颖的视角。
Card et al. (2007) 研究美国城市街区种族构成变化的“倾覆点” (tipping point)。这个概念引起经济学者的注意,最早始于Thomas Schelling (1969, 1971)。它是指城市里的街区一旦少数族裔的比例达到了“倾覆点”,白人居民会加速地搬出该街区,最终致使街区成为少数族裔聚居的地方。Schelling早就指出,一些看似不重要的偶然事件足以把一个街区推过这种临界点,引起剧烈的变化。他的这个研究影响很大,其中的洞见被应用到很多别的领域甚至被写进了畅销书(Gladwell, 2001)。Card et al. (2007) 用一个简单的模型,演示在什么情况下会出现街区种族构成的“倾覆点”,并用美国的人口普查数据来估计每个城市的“倾覆点”,看它与哪些城市的特点是相关的。
上面提到的后两篇文章用的数据是常见的普查数据,统计分析方法相当简单,在因果识别方面没有任何创新。这样的文章被顶级期刊接受发表,主要是两者都在分析重要的学术问题。严格说来,这两篇文章涉及的理论问题用纯文字的语言也可以讲清楚。但是模型的使用¾两篇文章都是既用了图表又用了方程式¾无疑让作者们把问题说得更清晰、简洁、逻辑严谨,让读者更容易认识到实证分析的必要性。
▷模型可以给新观察到的现象一个严谨的解释
正如上面提到的,经济学家常常把记录和解释现象合并在一起来做,而解释现象时往往需要借助于模型。上面提到的Eeckhout (2004) 就是这样的研究。作者首先用数据表明美国的城市人口规模服从对数正态分布,然后用一个模型来解释为什么会是这样的。
Knoll et al. (2017)也是类似的套路。他们收集了14个发达国家在1870-2012年间的年度房价,发现二十世纪中期以前各国住房的实际价格普遍比较稳定,此后都经历了长时间的大幅度的上升。作者们认为这不是建筑成本上升的结果,而是由地价上涨造成的。他们写了一个模型,具体解释二战以后什么原因导致地价的攀升进而推高了房价。
▷模型可以导出更合理的度量方法
城市和区域经济学关注的一个核心问题是经济活动的集聚,有不少实证研究需要度量每个行业的集聚程度。早期的研究使用的度量方法多是临时现抓的(ad hoc),譬如在区域的水平上计算每个行业的赫芬达尔—赫希曼指数(Herfindahl-Hirschman Index),用于衡量集聚程度。可是这样的算法缺乏深入的思考,和集聚的理论没有关联,有不少缺点。打个比方说,一个岛国只有两个大小一样的岛屿,A和B;甲行业有三个企业,每个企业有1000个雇员,其中有两个企业坐落在岛A、一个在岛B;乙行业有3000个企业,每个企业有一个雇员,其中有2000个企业坐落在岛A、1000个在岛B。如果用传统的度量方法,简单地看从业人员的分布,这两个行业的集聚程度类似,都有三分之二的雇员在岛A。可是我们不难想象,甲行业的结果有可能是随机的,并不一定表明岛A有更适宜的条件;而乙行业就不同了,几乎可以肯定有某种原因导致更多的企业出现在岛A。Ellison和Glaeser (1999) 通过一个模型导出集聚的程度应该如何度量更合理,能够剔除类似于上面这个例子中企业规模的影响;他们用新发明的度量方法重新来看美国各个行业的集聚程度。这个方法在后来的实证研究中被广泛地采用(例如Rosenthal和Strange, 2001)。
种族隔离是多个社会科学领域长期关注的问题,城市和区域经济学者一直致力于居住隔离的研究。早在1980年代,社会科学研究中用过的各类度量隔离程度的方法已经不下二十种(Massey和Denton, 1988),几乎都是研究者临时拟定的,没有任何理论基础。Echenique和Fryer (2007) 提出了一个新的度量方法。他们采用了数学家常用的公理化的方式,首先给出了一个度量隔离程度的方法需要具备的三个特点:(1) 更频繁的同种族交往意味着隔离程度的增加;(2) 隔离程度只跟个人层面的同种族交往的比率有关而与城市的大小无关;(3) 每个人的隔离程度都和他所交往的人的隔离程度线性相关。作者接着通过模型推导证明了,这三个条件决定了一个唯一的隔离指数。他们考察这个新的指数与此前常用指数的相关程度,并用这个新指数研究学校里朋友关系网的种族隔离程度以及城市里种族间的居住隔离程度。
▷模型能指导回归分析中函数关系的设定

我们如果在实证研究中做回归分析,经常要做函数关系的假设:确定哪些变量应该包括在要估计的函数里、它们之间是什么样的函数关系。理论模型经常对函数关系的设定有指导意义。譬如Arzaghi和Henderson (2008),他们以纽约的麦迪逊大道为例来测量集聚效应。麦迪逊大道常被用作美国广告业的代名词,是个广告业公司林立的地方。因为信息对广告业至关重要,靠近同业的公司在这个行业想来应该特别有利,所以作者选择这个行业来研究。他们对一个地方(Census tract) 一段时间内新生的广告公司数目进行回归分析。右边变量包括该地点商业企业总和,以及0-250米、250-500米、500-750米、750-1000米、1000-1250米范围内的广告公司数量,用以估算整体和同业的集聚效应。除了这些右边变量之外,作者只用了一个控制变量,就是地租。这是因为,作者假定新公司的诞生是利润高的表现,而理论模型里的利润明显是受地租影响的,所以地租必须作为控制变量出现在要估计的函数里。其它要素价格当然也影响利润,可是那些价格不太可能在很小的范围内有差别,就没有必要控制了。事实上,Arzaghi和Henderson (2008) 这个研究的重要发现之一是集聚收益大部分反映在地租上而不是在工资里,对此前用工资函数度量集聚收益的通行做法提出了质疑。
Glaeser et al. (1992) 也是一个例子。他们对城市里各行业就业人数的长期增长做回归分析,看三个不同的城市增长理论哪一个更有解释力。右边变量里用了专业化、竞争度、多样化三个指标来检验三个理论的不同含义。可是除了初始年代的就业量还需要加哪些控制变量呢?作者们用了初始年代行业内的工资水平。这是因为,他们写了一个简单的模型,发现就业增长是生产率增长和工资增长的函数,而专业化、竞争度、多样化三个指标都是通过生产率影响就业的,所以就需要在回归中加入工资一类的控制变量。
值得指出的是,这两个例子里的回归方程式应该包括哪些控制变量,如果脱离开模型去做取舍,都不是很容易决断的。而一旦在模型的框架下去思考,就发现作者们的选择是理所当然的。
▷模型能帮助澄清因果关系的传导机制
这里要举的几个例子,都是着重于识别因果关系的文章。正如Holmes (2010)所说的,这类研究试图通过“自然实验”来构造工具变量,生成外生的扰动,解决内生性的问题,从而估计一个变量对另一个变量的因果效应。因果识别做得巧妙的文章,估计出的因果效应较可信,但是无论多么巧妙的工具变量,都难以告诉我们因果效应是通过什么渠道起的作用。讲清楚究竟有哪些可能的渠道,归根到底还是个理论问题,这就给模型的使用提供了机会。
Boustan (2010) 研究美国的“白人群飞”(white flight)问题。二战以后,美国(特别是北方的)城市里有大量的白人家庭搬到郊区去住,一种说法认为白人对少数族裔抱有偏见甚至存在歧视、不愿意和少数族裔住在一个街区,他们搬到郊区去主要是为了躲避少数族裔占比越来越高的城市中心区。Boustan (2010)想考察一下这样的说法站不站得住脚。她利用南方郡县的自然条件来推测迁出农业的黑人总量,然后根据历史上的移民走向来推算迁入每个北方城市的黑人数量,进而看这个外生扰动是否影响白人家庭向郊区的搬迁。作者写了一个简单的居住地选择模型,假设家庭的效用取决于城里的黑人比例、便利条件和房价。从效用函数就马上可以看出,黑人家庭的迁入不但可以通过种族偏好,也可以通过推高房价影响白人家庭的搬迁。正因为如此,Boustan (2010)用相当多的篇幅来探讨“白人群飞”是否跟房价的变化有关。这个例子告诉我们,哪怕是一个极简单的模型,也有助于我们认清可能存在的因果效应传导机制。
Greenstone et al. (2010) 也是一篇在因果关系识别方面有所创新的文章。像中国的地方政府一样,美国的州县也常常从事招商引资的活动,有时甚至不惜巨额的补贴和税收减免来吸引大企业。首要原因当然是因为引来的企业直接创造就业和 (未来的) 税收,同时也是因为相信大企业的落户会对地方的其它企业有影响,带来所谓的“集聚溢出” (agglomeration spillovers) 效应。可是准确度量这个溢出效应的大小是相当困难的,主要是因为大企业可能会选择经济条件前景好的地方,所以该企业落户以后别的企业的良好表现可能是本来也会发生的。为了解决这个问题,Greenstone et al. (2010) 集中考察一些大型的“百万元级工厂” (“million dollar plants”), 其中每一个企业在选址期间都发生了多个地方争夺同一企业的现象。作者们就用争夺战中排名第二的地方作为对照组,跟这些大企业最终落户的地方对比来估算溢出效应。他们在进行数据分析之前,先用一个模型讲清落户的大企业会通过三种不同的渠道影响原有企业:一是增加原有企业的全要素生产率,即通常所说的知识溢出效应;二是推高用工成本;三是推高地价。后两者对原有企业的利润是负向的影响。正因为如此,看全要素生产率的变化是对溢出效应的直接检验。而看新企业数量的变化则是间接的、更严苛的检验;也就是说,如果大企业落户以后初创企业数量在增加,就意味着生产率方面的溢出效应大到足以弥补生产要素涨价的负向影响。依托于这样的模型,每一步的回归分析对应于哪一个机制的作用就可以表述得井井有条。
像这样的例子还有很多。但凡一个以因果识别为重点的实证研究,都需要探讨因果效应的机制。用模型来把各种可能的机制说清楚,是常用的做法。实证研究人员写模型的过程,就是一个深入思考传导机制的过程。
▷模型能给估计出来的系数赋予经济学上的含义
用商品价格对商品特征进行回归的做法,在实证经济学里由来已久。直到Rosen (1974) 给出一个模型,从消费者和供应商双方的优化行为中导出价格和特征的均衡关系,才算给特征回归 (hedonic regression) 提供了一个严谨的理论基础。后来Rosen (1979)和他的学生Roback (1982)又用类似的分析手段解释城市特征的隐性价格,成为城市经济学里很有名的Rosen-Roback分析框架,被认为是整个学科的理论支柱之一(Glaeser, 2007)。Roback (1982)从空间均衡的两个基本条件出发,假设在没有城际迁移成本的情况下规模收益不变的厂商无论在何处都挣得零利润、偏好相同的工人无论住在哪里都有同样的效用,以此导出一组颇具启发意义的结果。她的一个结论可以表示如下:
其中p*s代表消费者对城市特征的边际支付意愿,y是房产消费量,p是单位房产价格,w是工资水平。譬如s可以是空气质量, dp/ds和dw/ds可以用城市水平上的回归估计出来,y可以直接从数据中算得,三个数值合在一起,就能算出人们愿意付多少钱使得空气质量提高一点。这么一个简单的模型,一下子让三个本来只有统计意义的估值有了经济学上的含义。Chay和Greenstone (2005)利用美国空气清洁法案造成的外生扰动,以断点回归的方法估计空气质量对房价(和工资)的影响。他们正是借助于Roback的模型结果,来理解他们得到的参数的经济学意义。
再以我自己参与过的一项研究为例 (Brueckner et al., 2017)。我们有中国很多城市土地出让的数据,里面有出让前规划的容积率限制、出让价格、以及一些其它的相关信息。我们完全可以做这样一个题目:容积率影响地价吗?然后做如下的回归分析:
γ是地价,FAR是容积率(floor-to-area ratio),是一组控制变量。我们当然可以做一些因果关系识别方面的努力,譬如把临近的地块归入同一个组群并控制组群的固定效应,即通过对比组群内的地块来降低地块特征缺失可能造成的估计偏误。实际上我们确实做了这样的回归分析,但是在报告回归结果之前先写了一个模型。用S*代表没有管制情况下开发商自定的最优容积率,Sbar代表政府规定的容积率,那么S*/Sbar可以看作是管制严苛程度的指标,这个比率越高则管制得越严。因为现实中只有管制的情况存在,所以这个比率是无法观察到的。我们用一个简单的模型证明了,S*/Sbar这个比率越高,地价对容积率的弹性就越大。(这个关系很好理解,管制越严,放松一点管制对开发商的利润影响越大,他们就愿意出更高的价钱买地。)也就是说,地价对容积率的弹性也可以用来衡量管制的严苛程度,而依照方程(2)估计出来的系数β正是地价对容积率的弹性。如果我们不写这个模型,β能告诉我们容积率如何影响地价,只是一个有统计学意义的系数;而有了这个模型,同样的β就可以解释为管制的严苛程度,变成一个有经济学意义的概念了。也是因为这个模型,让一个原本只有研究土地或研究中国的几个小领域的学者会关心的回归分析,变成了关于管制严苛程度的这样一个有跨领域意义的题目。
作为这一节的小结,我在这里想强调几点。
第一,虽然我在讲解模型的每一个作用时用了不同的例子,这并不意味着一个模型在一篇论文里只能起到一个作用。事实上,一个模型经常在一项实证研究里起到多个作用。譬如说,一个模型完全有可能既有助于阐述一项研究的重要性,又能对回归方程的设定起指导作用。
第二,模型越简单越好。非结构性分析的目的不是估计模型的参数,使用模型总是为了讲清某个道理,而模型的建立就必须为这个目标服务。一般来说,能用简单的模型讲清楚的道理,就不应该用复杂的模型;能用一期的、静态的模型演示的变量关系,就不需要多期的、动态的模型;能用两要素的生产函数演示的替代关系,就没必要用多要素的模型。当然有时候我们需要检查由简化的模型导出的结果是否具有一般性,即便在这种时候,有很多学者也会选择在论文正文中只给出简单的模型,而把拓展部分放在附录里,以便减轻读者的负担。
第三,模型不但能帮助我们加深对某些问题的理解,更能帮助我们问出截然不同的问题。对于做实证研究的学者来说,写模型的过程就是从经济学的视角对研究对象加深理解的过程。我们一旦开始尝试从模型的角度思考问题,就必须直面每个相关决策者的偏好和约束,就必须去探索各种均衡条件下的结果,就必须要做到逻辑上的自洽。最终即便不需要把一个正式的模型写进论文,这样的思维练习也有助于增强研究的深度和严谨性。我曾经看到年轻同事的工作论文里对机制的讨论是不符合经济学逻辑的、甚至是自相矛盾的,这跟平时经常脱离、模型天马行空讨论问题的习惯应该是有关的。但愿上面这些例子足以说明,如果我们总是做不用模型的实证研究,那么我们所能提出的问题也是有限的。
05. 模型与结构性的实证研究
▷结构性的回归分析
结构性的回归分析总是要估计模型的参数,从定义上来说,这类实证研究一定会用到模型。这类研究估计的往往是“深度参数”,即那些相对稳定的、不随环境和时间变化的、决定个人和企业行为的参数,譬如消费者效用函数里的参数、企业生产函数里的参数、消费者的时间贴现因子、风险偏好系数等等。估计这些参数,往往是为了做反事实分析(counterfactual analysis),假设一个与事实相反的状态(某个事件发生了或没有发生、某个政策实施了或废止了),看看模型推测的结果是什么样的,与观察到的事实做比较,从而得出事件或政策的影响。
正是因为可以做反事实分析,结构性的回归能够帮助我们量化尚未发生的事件或政策的影响。相对于简化型估计,这是结构性估计的优势之一。举个例子来说,我们用双重差分或者随机实验的办法,估计了每一条新的公共汽车线路能减少的开私家车上班的人数。假设我们在因果识别方面做得无懈可击,得到的参数非常有说服力,那么再开通一条公汽线路会有何种影响,我们就比较有把握。可是如果我们要开通一条全新的地铁线路呢?从研究已有的公汽线路的作用得到的结果能用吗?毕竟地铁的速度、舒适程度、停靠站频率都跟公汽有很大差别。这种情况下就能显示出结构性回归的优势了,我们用一个实例来说明。
1970年代初,旧金山地区在建设一个全新的地铁系统(Bay Area Rapid Transit,BART)。政策制定者们自然想知道建成以后会有多少人上下班改乘地铁。官方雇佣的咨询机构用宏观的通勤流量做了估算,预计BART开通之后会分流15%的上下班出行人数。加州大学伯克利分校的经济学教授Daniel McFadden也研究了这个问题。他假设每个人有这样一个效用函数:
一位具有个人特征Zn的通勤人员如果选择了具有特征Xi 的通勤模式i,那么他的效用包括一个确定的部分X'iβ+Z'nγ和一个随机的部分εin。这个随机的部分可以看作是研究人员观测不到的个人特征和通勤方式特征的影响。如果我们假定εin服从IID的Gumbel (type I extreme value)分布,而且每个人都追求效用最大化,那么一个人选择通勤方式的概率有如下的解析表达式:
这样就可以通过最大似然法来估计效用函数的参数和。McFadden和他的助手对700多位湾区的通勤人员做了问卷调查,并用所得的数据估计出效用函数。因为每个通勤方式都被看作多个特征的组合(包括等车时间、乘车时间、换乘次数、等等),即便还没开通的地铁也可以被看作这些特征的组合,只不过有不同的特征值而已,可以通过效用函数计算它能带来的效用。用这样的方法,McFadden的团队预测将会有6.3%的通勤人员乘坐BART。地铁开通后调查发现的实际比例是多少呢?6.2%。方程(3)和(4)便是我们今天熟知的Logit模型,它不但一直是运输经济学领域常用的模型,而且被推广到很多其它的经济学领域(Small et al., 2005; Train, 2009)。
此后以Logit为基础的离散选择模型不断发展,到1995年有三位产业组织领域的学者发表了一篇极具影响的文章,分析消费者对不同品牌汽车的选择(Berry、Levinsohn和Pakes, 1995,通常被简称为BLP)。BLP假设消费者的效用是收入、汽车价格和汽车品牌特征的函数,外加一项随机扰动。他们延用随机效用服从Gumbel分布的假设,本质上仍然是一个Logit模型。但是三位学者引入了一系列的新思路,包括:让效用函数的参数随消费者个人特征变化;利用收缩映射(contraction mapping)的特性通过迭代运算估计不随个人特征变化的参数,以降低运算成本;分两步估计函数中非线性和线性部分的参数,在线性估计部分使用工具变量解决价格受缺失特征影响的内生性问题;在不知道个人选择的情况下通过匹配市场份额来估计个人效用函数中的参数,从而降低了对微观数据的要求。因为BLP的方法比较灵活,被后来的学者广泛采用。
Bayer et al. (2007) 用BLP的方法研究旧金山地区的居民对住房的选择。他们估计的效用函数除了包括住房特征和价格,还包括学区质量、种族构成等邻里特征。这样就可以通过估计出来的参数计算边际替代率¾增加一单位的邻里特征与放弃多少收入对效用的影响能互相抵消¾从而算出居民对邻里特征的支付意愿。为了消除邻里特征缺失而可能导致的偏误,Bayer et al. 一方面采用了Black (1999)的边界断点方法,即通过对照学区边界两侧的住房需求来控制缺失的邻里特征的影响;另一方面用3英里之外的房屋和街区特征做房价的工具变量(因为竞争关系而影响房价,但是不直接影响效用)。
Bayer et al. (2007) 和Black (1999) 同样都研究了居民对学区质量的支付意愿,前者是结构性估计,后者是简化型估计。对照这两项研究能让我们认识到两种方法的一些优缺点。Black (1999) 用的是传统的特征回归,学区质量的系数是边际购买者的支付意愿,可是如果想做成本效益分析来指导政策,我们需要的是平均支付意愿,Black的估值理论上来说并不适用;而Bayer et al. 的估计因为允许参数随个人特征变化,就可以估计平均支付意愿,对政策的指导意义更大。同样因为Black用的是特征回归,她的估值只能解释成对微小变化的支付意愿;而Bayer et al. 直接估计出了效用函数,可以用于计算对非边际变化的支付意愿。当然简化型估计也有它的优点,主要是计算相对简单,可以做很多敏感性和稳健性的检验。
Wong (2013) 用BLP的方法研究新加坡居民对住房的选择,着重研究对街区族裔构成的偏好,把街区内各族裔的居民比例直接纳入效用函数。新加坡有个种族配额制度,当一个小区某个族裔的比例达到规定的上限时,其他族裔的房主就不许把房子卖给这个族裔的居民了。Wong利用这个政策造成的需求上的“弯折”来帮助识别模型的参数。她实际上没有个人层面的信息,只是通过电话黄页上的姓名估算出各个小区的族裔比例,加上一些小区层面上的信息,用模拟广义矩的方法(simulated generalized method of moments)估计出个人效用函数的参数。这也反映出BLP方法对微观数据要求不高的特点。Wong (2013)还做了反事实分析,用估算的效用函数推算最优的族裔构成安排,然后看现实是否接近最优的安排。这也是上面提到的结构性研究的优势。

BLP的方法也被借用来研究跨城市的居住地选择,把城市特征写进效用函数。Bayer et al. (2009)利用美国国内移民走向来估计效用函数,研究人们对空气质量的显示性偏好。Zhang和Zheng (2015)用类似的方法研究人们对城市水平上的种族居住隔离的偏好,估算人们对降低隔离程度的支付意愿。值得一提的是,此前的研究者在估算人们对城市特征的支付意愿时,一般会使用上面提到的Rosen-Roback分析框架,这个方法的前提是城际迁徙成本为零,研究美国这样高度自由的社会里的问题也许还可以,借用到像中国这样的有迁徙限制的社会就有点勉强了。而BLP的方法就不需要零迁徙成本的假设,甚至可以把迁徙成本写进效用函数,直接去估计它的影响。正是因为此一方法的这个特点,Timmins (2007)用它研究了巴西的问题,Xing和Zhang (2017)、Freeman et al. (2017)用它研究了中国的问题。
最近几年来城市和区域经济学领域应用最广泛的结构性分析框架,是由贸易经济学家Eaton和Kortum (2002)首创的,今天经常被简称为EK模型。他们创建这个模型本来是用于分析国际贸易成本的影响。可是如果把原模型里的国家理解成一国之内的各个地区,就提供了一个分析区域经济的框架;如果把国家看作是城市里的街区,就成了分析城市经济的模型。前一类研究包括Donaldson和Hornbeck (2016) 关于铁路系统对美国经济的贡献的论文、Donaldson (2018) 关于印度的铁路系统对经济的影响的论文;后一类研究包括Ahlfeldt et al. (2015) 利用柏林墙的建立和拆除造成的外生扰动来估计城市内密度经济的论文,Tsivanidis (2018) 关于波哥大公交系统的影响的工作论文。一些学者也在用这个模型来研究中国的区域经济问题(Tombe和Zhu, 2017;Fan, 2017)。
EK模型是个一般均衡的框架,既设定消费者偏好、生产技术,又要处理消费品和要素市场的均衡,在这里没法给出一个完整的例子。但是有必要看一看此类模型对消费者的效用函数是如何设定的,以便能了解这类模型的一个重要特点。我这里以Ahlfeldt et al. (2015)为例,假设一个在街区居住、在街区j工作的消费者有如下的效用函数:
其中Ai 是街区i的便利条件,wj 是街区j 的工资水平,γi 是街区i 的房租水平,是两地之间的通勤成本。Zij 是随机效用冲击,服从Fréchet (type III extreme value)分布:
这里的Ti 是住在街区i得到的平均效用水平,Ej 是在街区j工作得到的平均效用水平,是个形状参数。ϵ>1 效用最大化可以导出一个人在街区i 居住、在街区j 工作的概率是:
就像Logit模型一样,这里通过对随机效用分布的假设,可以得到一个概率的解析解。当个人数量足够多时,这些概率加总就等于在街区居住、在街区j工作的城市人口比例。因而同样可以用最大似然法估计方程(7)里的每一个参数。跟Logit模型不同的是,这里选择的是两个地点的组合,而不是单个的地点。Fréchet分布是保证方程(7)解析解存在的关键条件,是每个EK模型里的核心假设。
上面几个例子都是关于效用函数的结构性估计,最后再举一个估计生产函数的例子。Epple et al. (2010) 试图估计住房的生产函数。这个问题的难处在于住房的数量是没法直接度量的,解决这类问题的传统方法是把产品价值加总用来表示产品总量。可是当产品的质量千差万别时(住房就是),这样的度量方法容易导致巨大的偏误。Epple et al. (2010) 从基本的微观理论出发提出了一个方法,即先估计建筑企业的利润函数,根据包络定理,利润函数的一阶导数是供给函数,而从供给函数可以导出生产函数。他们用匹兹堡地区的数据来演示这个方法的运用。作者们虽然没有做反事实分析,这样的估计结果显然对政策评估有用。不少地方政策(譬如地产税的变化、学区质量的提升)会影响住房需求,结合住房供给函数可以算出对房价的影响,进而推导出对本地居民福利的影响。
▷结构性的校准分析
有一些结构性的实证研究用的模型相当复杂,去估计模型中的每一个参数和变量关系已经不太现实。在这种情况下,研究人员可能去借用相关研究中得到的结果给模型参数赋值,对模型和参数值做出调整以使它模拟出的结果与现实中的一组事实大致吻合,然后用这个模型做模拟实验、反事实分析,以回答研究者关心的问题。这样的实证研究方法被称作校准(calibration)分析。校准最初被大量运用于分析一般均衡框架下的宏观经济问题。不难想象,宏观经济学问题涉及的决策者和部门较多、需要考虑的参数和变量关系也更多,因而完全依靠估计来给模型赋值极其困难,这是导致校准分析最先在该领域流行起来的原因之一。而宏观经济学家对城市和区域经济学问题的关注(例如Lucas和Rossi-Hansberg, 2002),自然就把这样的分析手段引入了城市和区域经济学。
做校准分析的实证研究一般分以下五个步骤进行(Kydland和Prescott 1996;DeJong和Dave, 2011,第六章):
(1) 提出一个需要定量解答的问题;譬如说,废止户籍制度对中国经济会产生怎样的影响?
(2) 选取一个前人检验过的合适的理论框架来回答这个问题;譬如说,可以用我们上面提到过的EK贸易理论框架。
(3) 建立一个模型,即由一组方程式来代表一个简化的经济体。
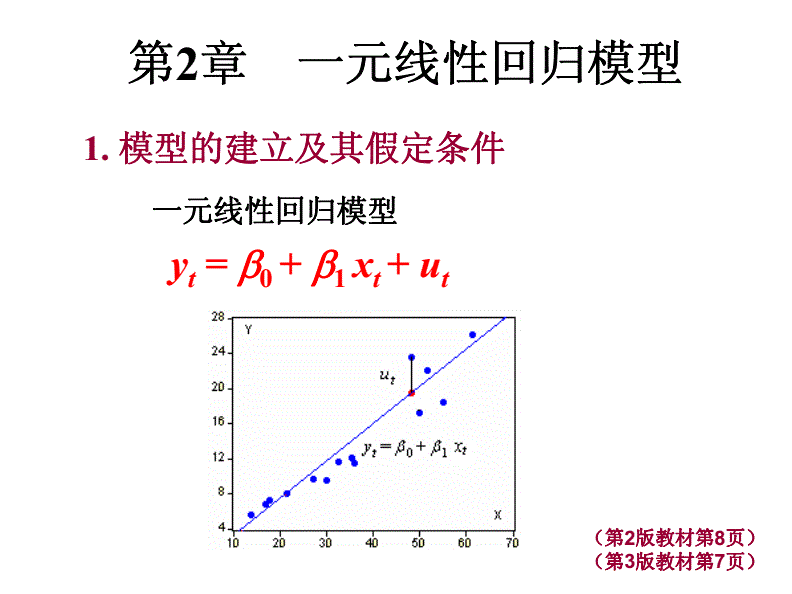
(4) 对模型进行校准,即给模型的参数赋值、选取特定的参数值组合以使模型模拟出的结果在事先选取的几个维度上跟现实大致吻合;譬如说,使模型计算出的经济增长率、进出口增长率、城市化率、城市规模分布变化等都跟数据里的趋势大致相同。(跟回归分析不同的是,校准分析在选择参数时不以最佳拟合程度为目标。校准模型的工作更像对仪器的调整,就像我们制做一个温度计,需要让它在热水开始沸腾之际显示100度、在冷水开始结冰之际显示零度;对模型的校准就是要让它产生的数量关系和特征符合已知的重要事实。)
(5) 用经过校准的模型做实验来回答步骤(1)里提出的问题,譬如说把模型中户籍制度的限制全部消除,看重新解出的宏观经济变量与废除限制之前有哪些变化;这样的练习不但能量化取消户籍制度对每一个宏观变量的影响,还能帮助研究者搞清楚这些影响是通过哪些渠道达成的。
Albouy (2009)就是使用校准分析的一个例子。作者要研究的问题是,美国的联邦所得税率对全国各地的居民是一致的,但是因为城市地区需要高收入来抵消高房价等高生活成本,导致城市地区的居民在累进税制的情况下税负更重。那么这种地区间的税负不平等的影响是什么呢?Albouy把收入所得税引入传统的Rosen-Roback理论框架,建立了一个一般均衡模型,对模型进行校准,然后用这个模型进行模拟实验。他发现,税负的不同导致高工资地区的长期就业水平被压低了13%,地价和房价被分别压低了21%和5%,由此而导致的经济损失占国民收入的0.23%。
Desmet et al. (2018) 研究未来世界经济发展的地理分布。他们将Allen和Arkolakis (2014)、 Eaton和Kortum (2002)以及Kline和Moretti (2014)等几个理论框架的特点结合起来构建一个一般均衡模型,用来分析地球上每个1经度´1纬度(在赤道附近大致等于111公里´111公里)的方格里的经济活动。他们对这个模型进行校准,通过该模型反推回去的人口分布与全球过去一百多年的人口分布和增长拟合较好。他们用这个模型来分析,如果世界范围内降低(国内的和跨国的)迁徙限制结果会怎样。他们发现,如果完全消除移民限制,全世界的福利会增长三倍,70%的人口会选择跨国移民。这样世界大同的极端情况当然不太可能实现,但是确实说明了对人力资本流动的限制影响何其大。他们也分析了部分地降低移民限制的影响以及不同地区所受影响的差异程度。
需要指出的是,即便是以校准分析为主体的实证研究,也经常用到各种回归方法。大致有以下三种情形:
(1)有些研究会先借助回归分析描述一些“典型事实”(stylized facts),然后以这些事实为指导建立模型,再针对模型做校准分析。譬如Felkner和Townsend (2011)关于泰国企业地理分布的研究,就先做回归来展示离市场和基础设施越近的地方企业数量越多、自然条件越好的地方企业数量越多等等,而后构建和校准模型的目标之一就是能说明这些事实。再比如Ngai和Tenreyro (2014)在研究住房市场的季节性变化时,先做回归显示春夏两季搬进新居的人家住的时间更久、翻修花费更低,表明春夏两季买到手的住房更合意,然后根据这些事实建了一个搜索匹配模型做校准分析。
(2)有很多研究在做校准分析时,用的一些参数值是研究者自己通过回归分析得到的。例如Albouy (2009) 在校准分析中采用的美国各城市工资水平,就是他自己通过回归分析估计的。Xu (2018)校准一个经过拓展的EK模型,分析中国高铁系统的福利效应,他用到的国内迁徙和贸易成本都是自己估计的。
(3)有些研究者在建立一个模型之后,先做回归分析来验证模型的某些推断,然后再做校准分析来回答所关心的问题。Rossi-Hansberg et al. (2010)关于住房外部效应的研究就是这样的,他们先建立一个模型来解释政府资助的城市改造项目的影响,然后用里士满的数据做非参数回归、显示城市改造项目对地价的影响随距离递减,最后做校准分析算出住房外部效应随距离递减的速率并计算城市改造项目的收益率。Gennaioli et al. (2013) 研究影响区域发展的因素,也是先根据模型的推断做回归分析、发现人力资本在解释区域收入差异时至关重要,然后再做校准分析,计算工人的教育水平、企业家的教育水平、人力资本外部性在解释区域间劳动生产率差异时各自起的作用。
▷结构性实证研究的优缺点
在结束这一小节之前,我仍然要做几点评论。在谈具体例子的时候,我已经提到一些结构性研究的优缺点,这里算是几点补充。
第一,有一种看法认为结构性研究的假设太多,不像简化型估计那样干净。这当然与结构性研究用到的模型相对更复杂有关。值得一提的是,所说的结构性研究假设太多在很大程度上只是一个错觉。任何一个试图解释现象或建立因果关系的实证研究,必然以一系列的假设为起点。举个例子来说,如果你的研究目的只是想说明厦门的住房均价比成都高,那你对比两个样本均值就行了,不用做太多的假设。可是一旦你想说明为什么厦门的房价更高,你必然要做一连串的假设。也就是说,即便是非结构性的研究,只要作者不是做简单的描述,一定也是建立在层层假设之上的。如果说结构性研究和非结构性研究在这一点上真有区别的话,那只是结构性研究因为有模型的约束必须在每一步尽量把假设讲清楚,而非结构性研究(特别是那些脱离模型的)往往做了很多隐含的假设。从科学研究的角度来说,写明所做的假设是个好习惯。
第二,另有一种观点认为,简化型研究在因果识别方面做得比结构性研究更好。这一点可以商榷。应该承认,强调因果关系的识别、要求研究者讲明外生扰动来源这样的标准做法,最早是由做简化型研究的学者大力推行的,而好的简化型研究确实在这一方面值得称赞和效仿。可是讲明外生扰动来源其实是每个做实证研究的学者都应该特别注意的,而最近这些年来做结构性研究的学者也已经接纳了这个标准。可以说,好的结构性研究在因果识别策略方面所下的功夫并不比好的简化型研究逊色。譬如前面提到的Ahlfeldt et al. (2015)利用柏林墙的起落、Wong (2013)利用新加坡的族裔配额、Bayer et al. (2007) 利用学区边界断点,都是很精彩的识别策略。
第三,简化型研究跟结构性研究比起来,因为计算量较小而更容易做稳健性、敏感性的检验。这是个不争的事实。自从Leamer (1983)倡导系统化的稳健性检验,实证经济学家在实践中应该说有了一些进步,现在很多微观实证研究会有专门的一节报告稳健性检验的结果。可是结构性研究在这方面还亟待提高。因为参数较多、计算繁复,很多结构性研究在挑战计算技术的极限,难以进行全面的稳健性分析,给人一个黑匣子的感觉、不知道计算结果对一些参数值有多么敏感。希望将来在计算技术继续提高的情况下,结构性研究能够进一步克服这方面的问题。
第四,因为与经济理论联系紧密、环环相扣,结构性的研究在一些学者看来更有趣。何为有趣,当然属于主观判断。但是也无法否认,有些研究的特点确实对学者具有更大的吸引力,譬如简洁的模型、意料之外而又在情理之中的结果、巧妙的计量方法设计等等,都是学者们普遍接受的好的研究所具有的特性。结构性的研究把经济学理论和统计分析有机地结合在一起,确实是一个较好的做法。譬如McFadden用一个并不很牵强的关于随机效用分布的假设,把效用最大化、最大似然法、边际替代率等经济学和统计学概念揉成一个整体,回答人们关心的实际问题,给人一种赏心悦目的感觉。
第五,结构性的方法能让我们提出不一样的问题、回答不同的问题。抛弃了模型,就等于抛弃了这一类问题。再以Au和Henderson (2005)为例,他们问中国的城市是不是太小了。我想没有人会否认这是一个极其重要的问题,关于这个问题的讨论从来没有停息,而对这个问题的回答关乎中国城市化道路的选择。同时我想受过严格训练的学者里也不会有人否认,这个问题不依靠模型是没法解答的。我们必须要搞清最优的城市规模是什么,然后与现实做对比,才能回答这个问题。也就是说,只有做结构性的估计才能回答这一类的问题。上面提到的,量化废止户籍制度的影响,也属于这类问题 (Bosker et al., 2012)。
06. 总结
回到开篇时提到的现象,我感觉很多城市和区域经济学领域的年轻华人学者都在做不用经济学模型的研究。我们经济学家知道分工的重要性,从个人的角度来看,如果觉得写模型不是自己的比较优势,从而致力于脱离模型的实证研究,似乎也是有道理的选择。可是如果一个群体都做这样的选择,就不正常了。我希望上面的这些例子能够表明,脱离正规理论模型会影响实证研究的深度、会限制我们选题的广度,把一大堆重要的问题排除在我们的研究之外。打个比方说,模型是我们经济学者探索未知世界的重要工具之一,放弃了这个工具就如同木工只留下了锤子而扔掉了改锥,手里的工具决定了我们只能看到钉子的用途而看不到螺丝钉的用途;更糟糕的是,我们可能由于手里工具的限制,去用锤子敲打螺丝钉。一个真正的学者,必然因问题的不同而选择最合适的解决方法(合适的工具)。如果能把各类研究方法的优势结合起来,就更好了。
我们华人经济学者,特别是研究中国问题的华人经济学者,大多有一个想法,就是通过自己的研究来理解中国的高速发展。我们时常说,用我们的研究讲好“中国的故事”。在经济学说史上有颇多建树的George Stigler (1960) 有个观点,他认为经济科学的重大发展,主要是由学科内的逻辑运行机制推动的,现实世界的具体事件起的作用有限。中国的高速发展无疑是几十年来经济领域最重要的现象之一,这也是我们很多华人学者做研究的动力之一。可是按Stigler的说法,研究了身边重要的现象并不必然是重要的研究;只有在研究这个现象时推动了学科的发展,才能成为重要的贡献。换句话说,只有把“中国的故事”讲成“经济学的故事”,以中国的经验推动学科内知识的积累和方法的创新,才有可能做出有影响的学术贡献。在我看来,以模型为依托的实证研究,是从“中国的故事”里提炼经济学时不可或缺的一项工作。








