图像分割是一种重要的图象剖析技术。对图象分割的研究仍然是图象技术研究中的热点和焦点。医学图象分割是图象分割的一个重要应用领域,也是一个精典困局,至今已有上千种分割方式,既有精典的方式也有结合新兴理论的技巧。
本论文首先介绍了双峰法以及最大类残差手动阈值法,然后重点介绍一种基于小波变换的图象分割方式,该方式先对图象的灰度直方图进行小波多尺度变换,然后从较大的尺度系数到较小的尺度系数逐渐定位出灰度阀值。最后,对这几种算法的分割疗效进行了比较。实验结果表明, 本设计才能实时稳定的对目标分割提取,分割疗效良好。
医学图象分割是医学图象处理中的一个精典困局。图像分割才能手动或半自动勾勒出医学图象中的解剖结构和其它感兴趣的区域,从而有助于医学确诊。
1.1 图像分割技术的现况和发展情况
图像分割算法的研究已有几十年的历史,一直以来都深受人们的高度注重。关于图象分割的原理和技巧国内外已有不少的论文发表,但仍然以来没有一种分割方式适用于所有图象分割处理。传统的图象分割方式存在着不足,不能满足人们的要求,为进一步的图象剖析和理解带来了困难。随着计算机技术的迅猛发展,及其相关技术的发展和成熟,结合图象提高等技术,能够在计算机上实现图象分割处理。
其中最主要的技术是图像分割技术,从图象上将某个特定区域与其它部份进行分离并提取下来的处理。图像分割的方式有许多种,有阀值分割方式,边界分割方式,区域提取方式,结合特定理论工具的分割方式等。早在1965年就有人提出测量边沿算子,边缘检查已形成不少精典算法。越来越多的学者开始将数学形态学、模糊理论、遗传算法理论、分形理论和小波变换理论等研究成果运用到图象分割中,产生了结合特定物理方式和针对特殊图象分割的先进图像分割技术。尤其是近些年来迅速发展上去的小波理论为图象处理带来了新的理论和技巧。小波变换具有良好局部特点,当小波函数尺度较大时,抗噪音的能力强,当小波函数尺度较小时,提取图象细节的能力强,这样就可以挺好地解决抑制噪音和提取图象边沿细节之间的矛盾。
1.2 图像分割主要研究方式
图像分割是图象处理中的一项关键技术,自20世纪70年代起仍然深受人们的高度注重,至今已提出了上千种各类类型的分割算法,现提出的分割算法大都是针对具体问题的,并没有一种适合于所有图象的通用分割算法,而且近些年来每年都有上百篇相关研究报导发表。然而,还没有制订出选择合适分割算法的标准,这给图像分割技术的应用带来许多实际问题。因此,对图象分割的研究还在不断深入之中,是目前图象处理中研究的热点之一。
图像分割在图象工程中的位置它起着承上启下的作用,可以觉得是介于低层次处理和高层次处理的中间层间。最近几年又出现了许多新思路、新方式、或改进算法。下面对一些精典传统方式作简略的概述。
多年来人们对图象分割提出了不同的解释和叙述,借助集合概念对图象分割可给出如下定义:令集合R代表整个图象区域,对R的图象分割可以看做是将R分成N个满足以下条件的非空子集R1,R2,R3,…,RN;
(1)在分割结果中,每个区域的象素有着相同的特点;
(2)在分割结果中,不同子区域具有不同的特点,并且它们没有公共特点;
(3)分割的所有子区域的并集就是原先的图象;
(4)各个子集是连通的区域;
图像分割是把图象分割成若干个特定的、具有奇特性质的区域并提取出感兴趣目标的技术和过程,这些特点可以是象素的灰度、颜色、纹理等提取的目标可以是对应的单个区域,也可以是对应的多个区域。图像分割方式有许多种分类方法,在这儿将分割方式概括为四类:(1)边缘测量方式(2)区域提取方式(3)阈值分割方式(4)结合特定理论工具的分割方式。下面就这种方式展开介绍。
1.2.1 边缘检测法
图像剖析和理解的第一步往往是边沿监测。边缘测量方式是人们研究得比较多的一种方式,它通过测量图象中不同区域的边沿来达到分割图象的目的。边缘测量的实质是采用某种算法来提取出图象中对象与背景问的交界线。我们将边沿定义为图象中灰度发生急遽变化的区域边界。图像灰度的变化情况可以用图象灰度分布的梯度来反映,因此我们可以用局部图象微分技术来获得边沿检查算子。经典的边沿检查方式,是通过对原始图象中象素的某小邻域构造边沿检查算子来达到测量边沿这一目的。
1.2.2 区域提取法
区域提取法有两种基本方式:一种是从单个象素出发,逐渐合并以产生所需的分割区域;另一种是从全图出发,逐渐分裂切割至所需的分割区域。在实际中使用的一般是这两种基本方式的结合。根据以上两种基本方式,区域提取法可以分为区域生长法和分裂合并法。区域生长法的基本思想是将具有相像性质的象素合起来构成区域,具体做法是先给定图象中要分割的目标物体内的一个小块或则说种子区域,再在种子区域的基础上不断将其周围的象素点以一定的规则加入其中,达到最终将代表该物体的所有象素点结合成一个区域的目的。该技巧的关键是要选择合适的生长或相像准则。生长准则通常可分为三种:基于区域灰度差准则、基于区域内灰度分布统计性质准则和基于区域形状准则。分裂合并法是先将图象分割成好多的一致性较强的小区域,再按一定的规则将小区域融合成大区域,达到分割图象的目的。区域提取法的缺点是常常会导致过度分割,即将图象分割成过多的区域,因此近些年来针对这些技巧的研究较少。
1.2.3 阈值分割法
对灰度图象的取阈值分割就是先确定一个处于图象灰度取值范围之中的灰度阀值,然后将图象中各个象素的灰度值都与这个阀值相比较,并按照比较结果将对应的象素分为两类。这两类象素通常分属图象的两类区域,从而达到分割的目的。阈值分割算法主要有两个步骤:
(1)确定须要的阀值;
(2)将分割阀值与象素值比较以界定象素。
可以看出,确定一个最优阀值是分割的关键。现有的大部分算法都是集中在阀值确定的研究上。阈值分割方式依照图象本身的特性,可分为单阈值分割方式和多阀值分割方式:也可分为基于象素值的阀值分割方式、基于区域性质的阀值分割方式和基于座标位置的阀值分割方式.若考虑分割算法所用的特点或准则的特性,还可以分为直方图与直方图变换法、最大类空间方差法、最小偏差法与均匀化偏差法、共生矩阵法、最大熵法、简单统计法与局部特点法、概率松驰法、模糊集法等。
1.2.4结合特定理论工具的分割方式
近年来,随着各学科许多新理论和技巧的提出,人们也提出了许多结合特定理论工具的分割方式,例如基于数学形态学的分割方式,基于神经网路的分割方式,基于信息论的分割方式,基于模糊集合和逻辑的分割方式,基于小波分析和变换的分割方式,基于遗传算法的分割方式等。基于小波分析和变换的分割方式是利用新出现的物理工具小波变换来分割图象的一种方式,也是现今特别新的一种技巧。小波变换是一种多尺度多通道剖析工具,比较适宜对图象进行多尺度的边沿测量,例如可借助高斯函数的一阶和二阶导数作为小波函数,利用Mallat算法分解小波语音信号的小波分析仿真程序,然后基于马尔算子进行多尺度边沿检查,这里小波分解的级数可以控制观察距离的“调焦”。而改变高斯函数的标准差可选择所测量边沿的细节程度。小波变换的估算复杂度较低,抗噪音能力较强。理论证明以零点为对称点的对称二进小波适宜检查屋顶状边沿,而以零点为反对称点的反对称二进小波适宜检查阶跃状边沿。近年来多通道小波也开始用于边沿检查。另外,利用正交小波基的小波变换也可提取多尺度边沿语音信号的小波分析仿真程序,并可通过对图象奇异度的估算和恐怕来分辨一些边沿的类型。
由于图象的直方图可以看作是一维讯号,而直方图上的突变点(波峰点和波谷点),往往可以代表图象灰度变化的特点。因此Jean-Christophe Olivo提出了用小波变换对直方图进行处理的方式实现手动阀值提取。Olivo通过测量直方图小波变换的奇特点和区域极值点给出直方图峰值点的特点。而小波变换的波峰和波谷点可以代表图象中灰度代表值和阀值点。利用小波变换多尺度特点实现对图象的阈值分割。又因为小波变换具有多码率的特点,因此可以通过对医学图象直方图的小波变换,实现由粗到细的多层次结构的阈值分割。首先在最低码率一层进行,然后逐步向高层加快。小波变换的零交叉点表示了在帧率2j时低通讯号的局部跳变点。当尺度2j减少时,信号的局部微小细节渐渐增多,因此,能够测量出各微小细节的灰度突变点;当尺度2j减小时,信号的局部细节渐渐消失,而结构较大的轮廓却能清晰地反映下来,因而能测量出该结构较大的灰度突变点。因此,可以选择小波为光滑函数的二阶导数,对图象的一维直方图讯号进行小波变换,检测出直方图讯号的突变点,由此搜索出两峰之问的谷点作为分割阀值点。这就是小波变换用于图象分割的基本原理。对图象的直方图来说,它的各层的小波分解系数表示不同码率下的细节讯号,它与小波近似讯号联合构成直方图的多码率小波分解表示。给定直方图,考虑其多分辨率小波分解表示的零交叉点和极值点来确定直方图的峰值点和谷点。
多分辨率阀值选定
基于直方图和小波变换的图像分割技术由以下几个步骤组成:首先由粗码率下的图象直方图细节信息确定分割区域类数;其次,在相邻峰之间手动确定最优阀值;最后用求出的最优阀值分割原图象。
由于图象的原始直方图通常不够平滑或富含一定的噪音,因此,有必要对原始直方图进行平滑处理,以利于分割目标。其方式为:在空间域中采用保护边沿平滑方式平滑直方图,它既能保留原直方图基本变化特点,又能清除小峰的跳动。或者选定大尺度下的小波变换系数对直方图进行处理,也可以减少噪音的影响。
在帧率为2j时,由小波分解后的直方图近似讯号的极大值确定初始区域类数,即确定峰的数量。对于灰度级数不多的原始影 像,一个区域类一般对应直方图中的一个峰,然而,对于一幅复杂图象,经小波分解后平滑直方图中的每位峰则不一定都对应一个区域类,它也可能从属于毗邻的一个峰,因而有必要通过检测认定什么峰对应于分割区域类。
峰的独立性判定是为了清除不能成为一类的这些峰,独立峰应满足三个条件:
(1)应具有一定的灰度范围;
(2)应具有一定峰下面积;
(3)应具有一定的峰谷差。
峰与峰之间的谷点选定首先在最低帧率层进行,然后逐层推动,直到讯号的最高帧率层,并在每一层的阀值选定中,采用前一层的选定结构为引导。这种由粗到精的控制策略,能有效地选定最优分割阀值,同时较好地克服了噪音干扰和搜索空间大的问题。
设最优阀值分别为为T1,T2,T3,…,Tk(k为正整数),即可用这种最优阀值分割原始图象f(x,y),得到分割结果g(x,y),公式如下:
其中Ck(k=O,1,...,K)表示分割后的类别代码。
(a)小波分解
(b)小波分割 (c)传统分割
图4-10小波阈值分割
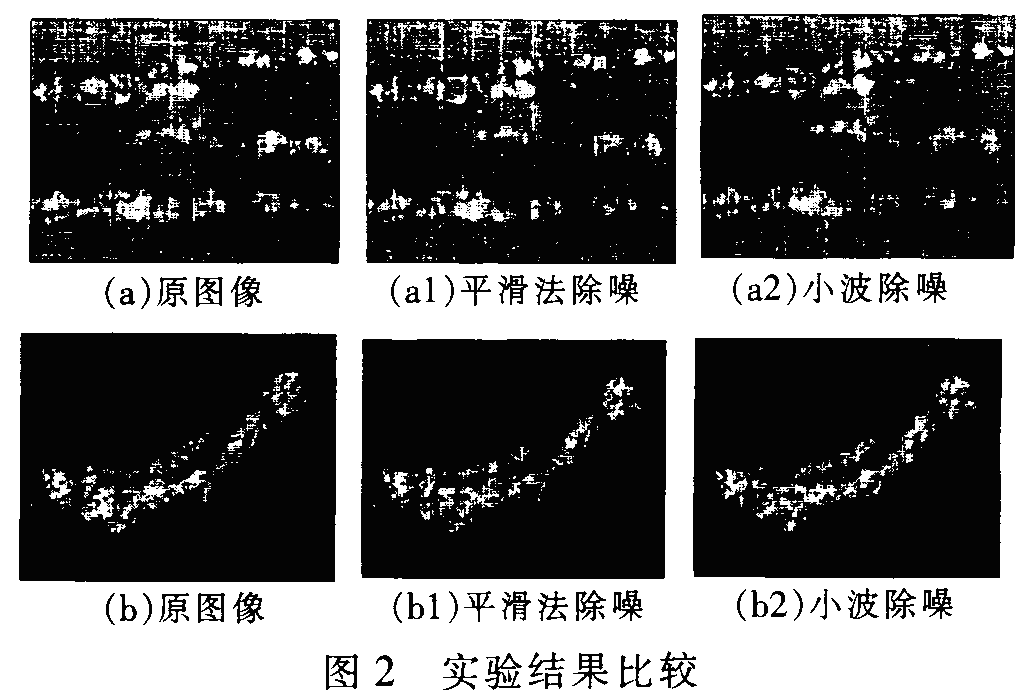
传统阈值分割与小波阈值分割方式的比较:
一、全局二值化方式因为采用的是用一个固定门限值来分割,因此门限值的选定非常重要。虽然诸多学者提出了许多种选定“最优门限”的方式,但这些分割方式在光照不均匀和须要提取多个复杂特点的物体的时侯无法获得较理想的疗效。自适应二值化方式因为采用了手动取阀值的方式,避免了采用固定阀值的弊端,但是图象分割后局限性太大,效果不佳。
二、基于灰度直方图小波变换的多阀值分割,在小尺度下受噪音影响较大,但对阀值的定位比较准;大尺度下受噪音影响较小,可以找到确定阀值。峰与峰之间的谷点直接在大尺度下进行,既克服了噪音的影响,又有效的选定到最优阀值。对图象分割的疗效显著优于前一种方式。
三、信噪比是讯号与噪音的功率谱之比,但一般功率谱无法估算,有一种方式可以近似恐怕图像杂讯,即讯号与噪音的残差之比。首先估算图像所有像素的局部残差,将局部残差的最大值觉得是讯号残差,最小值是噪音残差,求出它们的比值。信噪比越大,说明混在信号里的噪音越小,信号质量越好。
峰值信噪比通常是用于最大值讯号和背景噪声之间的一个工程项目。通常在经过影像压缩以后,输出的影像一般还会有某种程度与原始影像一样。为了评判经过处理后的影像品质,我们一般会参考PSNR值来认定某个处理程序够不够令人满意。PSNR值越大,就代表失真越少。
客观评价
分割方式
分割方式
TIME
SNR
PSNR
Threshold
双峰法
0.859649s
35.48
1.56
40
最大类方差法
0.242231s
35.18
1.26
62
小波变换
0.841680s
48.22
14.30
253
通常一幅图象分割结果的好与坏,以人的主观判定作为评价标准[13],也就是说是人的视觉决定了分割结果的优良,这样就造成了因为人的视觉差别对图象分割优劣评价的不统一,所以对不同分割方式的结果做一个定量的、定性的评价也是必要的且有意义的。
1、双峰法
tic;
I=imread('医学1.bmp');
A=I;%A=rgb2gray(I);
figure(1);
subplot(1,3,1);
B=imhist(A);
plot(B);
title('直方图');
subplot(1,3,2);
imshow(I);
title('原始图象');
[m,n]=size(I);
for i=1:m
for j=1:n
if(I(i,j)
I(i,j)=255;
else I(i,j)=0;
end
end
end
subplot(1,3,3);
imshow(I);
imwrite(I,'I.bmp');
title('阈值40分割图象');
toc;
%图像的MSE、SNR、PSNR的估算
B=I;
[M,N]=size(A);
a=double(A);b=double(B);
sum1=0;
for i=1:M;
for j=1:N;
sum1=sum1+(a(i,j)-b(i,j))^2;
end;
end;
mseValue=sum1/(M*N);%计算均方误差MSE
sum2=0;
for i=1:M;
for j=1:N;
sum2=sum2+(a(i,j))^2;
end;
end;
P=sum2;
snrValue=10*log10(P/mseValue);%计算时延SNR
psnrValue=10*log10(255^2/mseValue);%计算峰值信噪比PSNR
2、最大类间差法
tic;
x=imread('医学1.bmp');
subplot(1,2,1);
imshow(x) ;title('原始图象');
count=imhist(x);
[m,n]=size(x);
N=m*n;
L=256;
count=count/N;
for i=1:L
if count(i)~=0
st=i-1;
break;
end
end
for i=L:-1:1
if count(i)~=0
nd=i-1;
break;
end
end
f=count(st+1:nd+1); %f是每位灰度出现的机率
p=st; q=nd-st;
u=0;
for i=1:q
u=u+f(i)*(p+i-1); %u是象素的平均值
ua(i)=u; %ua(i)是前i个象素的平均灰度值
end;
for i=1:q
w(i)=sum(f(1:i)); %w(i)是前i个象素的累加机率
end;
d=(u*w-ua).^2./(w.*(1-w));
[y,tp]=max(d); %可以取出字段的最大值及取最大值的点
th=tp+p;
for i=1:m
for j=1:n
if x(i,j)>th
x(i,j)=0;
else
x(i,j)=255;
end
end
end
subplot(1,2,2);
imshow(x); title('最大类方差法');
toc;
%图像的MSE、SNR、PSNR的估算
A=imread('医学1.bmp');
B=x;
[M,N]=size(A);
a=double(A);b=double(B);
sum1=0;
for i=1:M;
for j=1:N;
sum1=sum1+(a(i,j)-b(i,j))^2;
end;
end;
mseValue=sum1/(M*N);%计算均方误差MSE
sum2=0;
for i=1:M;
for j=1:N;
sum2=sum2+(a(i,j))^2;
end;
end;
P=sum2;
snrValue=10*log10(P/mseValue);%计算时延SNR
psnrValue=10*log10(255^2/mseValue);%计算峰值信噪比PSNR
3、小波分割
clear;
tic;
imgname='医学1.bmp';
wavename='haar'; %用haar小波来分解
mode='per';
[x,map]=imread(imgname); %x是象素色值,map是色谱
figure(1);
subplot(2,2,1);imshow(x);
title('原图');
r=x; %r=rgb2gray(x) 三维图象弄成二维图象
xx=histeq(r); %直方图均衡化
subplot(2,2,2);imshow(xx);
title('增强后的图象');
deccof=struct('ca',[],'ch',[],'cv',[],'cd',[]); %三层分解
reccof=struct('rx',[]);
sx=size(xx);
nbcol=size(map,1);
dx=xx;
deccof(1).ca=xx;
[deccof(2).ca,deccof(2).ch,deccof(2).cv,deccof(2).cd]=dwt2(dx,wavename,'mode',mode); %使用小波函数对图象dx进行二维小波变换
figure(2);imshow([deccof(2).ca/255,deccof(2).ch/255;deccof(2).cv/255,deccof(2).cd/255;]);
title('小波分解');
am=deccof(2).ca/255;
figure(1);
subplot(2,2,3);imshow(am);
title('近似份量');
%找阀值
L=size(am,1);
W=size(am,2);
N=L*W;
[Count Ret]=imhist(am);
Pi=Count'./N;
g=[];
for t=0:255
w0=sum(Pi(1:t+1));
w1=1-w0;
mu0=sum(Pi(1:t+1).*(0:t))/w0;
mu1=sum(Pi(t+2:256).*(t+1:255))/w1;
mu=sum(Pi(1:256).*(0:255));
g=[g w0*w1*(mu0-mu1)^2/(w1*(mu0-mu)^2+w0*(mu1-mu)^2)];
end
[Ret1 T ]=max(g);
T1=T;
T=num2str(T-1);
disp(['最佳灰度threhold: ' T]);
%分割
I1=im2bw(am,T1/255);
figure(1),subplot(2,2,4);imshow(I1);
title('阈值分割后的图象');
u=idwt2(I1,deccof(2).ch/127,deccof(2).cv/127,deccof(2).cd/127,wavename,'mode',mode);
figure(3),imshow(u);title('小波分割图象') ;
toc;
%图像的MSE、SNR、PSNR的估算
A=imread('医学1.bmp');
B=u;
[M,N]=size(A);
a=double(A);b=double(B);
sum1=0;
for i=1:M;
for j=1:N;
sum1=sum1+(a(i,j)-b(i,j))^2;
end;
end;
mseValue=sum1/(M*N);%计算均方误差MSE
sum2=0;
for i=1:M;
for j=1:N;
sum2=sum2+(a(i,j))^2;
end;
end;
P=sum2;
snr=10*log10(P/mseValue);%计算码率SNR
psnr=10*log10(255^2/mseValue);%计算峰值信噪比PSNR









