求用matlab编BP神经网路预测程序求一用matlab编的程序P=[。。。];输入T=[。。。];输出%创建一个新的前向神经网路net_1=newff(minmax(P),[10,1],{'tansig','purelin'},'traingdm')%当前输入层残差和阀值inputWeights=net_1.IW{1,1}inputbias=net_1.b{1}%当前网路层残差和阀值layerWeights=net_1.LW{2,1}layerbias=net_1.b{2}%设置训练参数net_1.trainParam.show=50;net_1.trainParam.lr=0.05;net_1.trainParam.mc=0.9;net_1.trainParam.epochs=10000;net_1.trainParam.goal=1e-3;%调用TRAINGDM算法训练BP网路[net_1,tr]=train(net_1,P,T);%对BP网路进行仿真A=sim(net_1,P);%估算仿真偏差E=T-A;MSE=mse(E)x=[。。。]';%测试sim(net_1,x)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%不可能啊我200928对初学神经网路者的小提示第二步:把握如下算法:2.最小均方偏差,这个原理是下边提及的神经网路学习算法的理论核心,入门者要先看《高等物理》(高等教育出版社,复旦学院版)第8章的第十节:“最小二加法”。
3.在第2步的基础上看Hebb学习算法、SOM和K-近邻算法,上述算法都是在最小均方偏差基础上的改进算法,参考书籍是《神经网路原理》(机械工业出版社,SimonHaykin著,中英文都有)、《人工神经网路与模拟进化估算》(复旦学院出版社,阎平凡,张长水著)、《模式分类》(机械工业出版社,RichardO.Duda等著,中英文都有)、《神经网路设计》(机械工业出版社,MartinT.Hargan等著,中英文都有)。4.ART(自适应谐振理论),该算法的最浅显易懂的读物就是《神经网路设计》(机械工业出版社,MartinT.Hargan等著,中英文都有)的第15和16章。若看理论剖析较费力可直接编程实现一下16.2.7节的ART1算法小节中的算法.4.BP算法,初学者若对偏差反传的剖析过程理解费力可先跳过理论剖析和证明的内容,直接借助最后的学习规则编个小程序并测试,建议看《机器学习》(机械工业出版社,TomM.Mitchell著,中英文都有)的第4章和《神经网路设计》(机械工业出版社,MartinT.Hargan等著,中英文都有)的第11章。BP神经网路Matlab实例(1)分类:Matlab实例采用Matlab工具箱函数构建神经网路,对一些基本的神经网路参数进行了说明,深入了解参考Matlab帮助文档。
%例1采用动量梯度增长算法训练BP网路。%训练样本定义如下:%输入矢量为%p=[-1-231%-115-3]%目标矢量为t=[-1-111]closeallclearclc%---------------------------------------------------------------%NEWFF——生成一个新的前向神经网路,函数格式:%net=newff(PR,[S1S2...SNl],{TF1TF2...TFNl},BTF,BLF,PF)takes,%PR--Rx2matrixofminandmaxvaluesforRinputelements%(对于R维输入,PR是一个Rx2的矩阵,每一行是相应输入的边界值)%Si--第i层的维数%TFi--第i层的传递函数,default='tansig'%BTF--反向传播网路的训练函数,default='traingdx'%BLF--反向传播网路的残差/阀值学习函数,default='learngdm'%PF--性能函数,default='mse'%---------------------------------------------------------------%TRAIN——对BP神经网路进行训练,函数格式:%train(NET,P,T,Pi,Ai,VV,TV),输入参数:%net--所构建的网路%P--网路的输入%T--网路的目标值,default=zeros%Pi--初始输入延后,default=zeros%Ai--初始网路层延后,default=zeros%VV--验证向量的结构,default=[]%TV--测试向量的结构,default=[]%返回值:%net--训练以后的网路%TR--训练记录(训练次数及每次训练的偏差)%Y--网路输出%E--网路偏差%Pf--最终输入延后%Af--最终网路层延后%---------------------------------------------------------------%SIM——对BP神经网路进行仿真,函数格式:%[Y,Pf,Af,E,perf]=sim(net,P,PiAi,T)%参数与前同。
%---------------------------------------------------------------%%定义训练样本%P为输入矢量echoonP=[-1,-2,3,1;-1,1,5,-3];%T为目标矢量T=[-1,-1,1,1];%创建一个新的前向神经网路net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm')%---------------------------------------------------------------%训练函数:traingdm,功能:以动量BP算法修正神经网路的残差和阀值。%它的相关特点包括:%epochs:训练的次数,默认:100%goal:偏差性能目标值,默认:0%lr:学习率,默认:0.01%max_fail:确认样本进行仿真时,最大的失败次数,默认:5%mc:动量因子,默认:0.9%min_grad:最小梯度值,默认:1e-10%show:显示的间隔次数,默认:25%time:训练的最长时间,默认:inf%---------------------------------------------------------------%当前输入层残差和阀值inputWeights=net.IW{1,1}inputbias=net.b{1}%当前网路层残差和阀值layerWeights=net.LW{2,1}layerbias=net.b{2}%设置网路的训练参数net.trainParam.show=50;net.trainParam.lr=0.05;net.trainParam.mc=0.9;net.trainParam.epochs=1000;net.trainParam.goal=1e-3;%调用TRAINGDM算法训练BP网路[net,tr]=train(net,P,T);%对BP网路进行仿真A=sim(net,P)%估算仿真偏差E=T-AMSE=mse(E)echoofffigure;plot((1:4),T,'-*',(1:4),A,'-o')1BP神经网路的原理及算法的基本步骤理论上已证明,一个3层的BP网路才能实现任意的连续映射,可以任意精度迫近任何给定的连续函数。
1.1BP神经网路的原理BP(BackPropagation)神经网路一般由具有多个节点的输入层(inputlayer)、隐含层(hiddenlayer)和多个或一个输出节点的输出层(outputlayer)组成,其学习过程分为信息的正向传播过程和偏差的反向传播过程两个阶段。外部输入的讯号经输入层、隐含层为止。的神经元逐层处理,往前传播到输出层,给出结果。若果在输出层得不到期望输出,则转到逆向传播过程,将实际值与网路输出之间的偏差沿原连接通路返回,通过更改各层神经元的联接权重,降低偏差,之后再转到正向传播过程,反复迭代,直至偏差大于给定的值表11981~2005年全省总人口(单位:千人)年份198119821983198419851986198719881989人口99622101541102495103604104639106008108000109614111191年份199019911992199319941995199619971998人口114333115823117171118517119850121121122389123626124810年份1999200020012002200320042005人口125909缺省127627128453129227129988130756模型二预测2001年~2010年全省总人口(单位:千人)年份20012002200320042005人口127699128457129220129987130758年份20062007200820092010人口131534132315133100133890134685模型预测的全省总人口(1981年至2016年)(单位:千人)年份198119821983198419851991人口99266101308102967104600106203115172年份199219931994199520012002人口116550117895119205120480127403128436年份200320042005200620072008人口129437130405131340132244133116133958年份200920102015202020252030人口134770135552139049141921144257146144年份203520402045205020602070人口147659148869149832150596151678152352年份208020902100210521102120人口152769153026153185153240153283153344模型四预测2011至2020年人口(单位:千人)年份20112012201320142015全省总人口134668135478136325137185138036年份20162017201820192020全省总人口1388621396521404021411061417602.1借助MatlabScript节点实现在此以对一个非线性函数的迫近作为反例来说明实现流程,其中输入矢量p=[-1∶0.05∶1];目标矢量t=sin(2*pi*p)+0.1randn(size(p))。
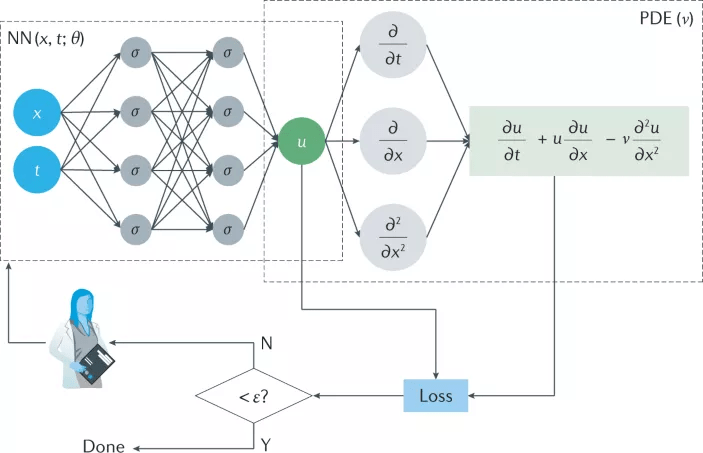
借助Mat-labScript节点实现BP算法的过程如下:(1)新建一个LabVIEWvi,在框图程序中添加MatlabScript节点。(2)在节点内添加Matlab的动量BP算法实现代码,并分别在节点左右边框分别添加对应的输入/输出参数,如图1所示。(3)在vi的前面板添加相应的控件,设置输入参数,联接输出控件。执行程序,结果如图2、图3所示。下边的代码将重建我们先前的网路,之后用批处理最速增长法训练网路。(注意用批处理方法训练的话所有的输入要设置为矩阵形式)net=newff([-12;05],[3,1],{'tansig','purelin'},'traingd');net.trainParam.show=50;net.trainParam.lr=0.05;net.trainParam.epochs=300;net.trainParam.goal=1e-5;p=[-1-122;0505];t=[-1-111];net=train(net,p,t);TRAINGD,Epoch0/300,MSE1.59423/1e-05,Gradient2.76799/1e-10TRAINGD,Epoch50/300,MSE0.00236382/1e-05,Gradient0.0495292/1e-10TRAINGD,Epoch100/300,MSE0.000435947/1e-05,Gradient0.0161202/1e-10TRAINGD,Epoch150/300,MSE8.68462e-05/1e-05,Gradient0.00769588/1e-10TRAINGD,Epoch200/300,MSE1.45042e-05/1e-05,Gradient0.00325667/1e-10TRAINGD,Epoch211/300,MSE9.64816e-06/1e-05,Gradient0.00266775/1e-10TRAINGD,Performancegoalmet.a=sim(net,p)a=-1.0010-0.99891.00180.9985用nnd12sdsd1来演示批处理最速增长法的性能。
推动量的批处理梯度增长法(TRAINGDM)net=newff([-12;05],[3,1],{'tansig','purelin'},'traingdm');net.trainParam.show=50;net.trainParam.lr=0.05;net.trainParam.mc=0.9;net.trainParam.epochs=300;net.trainParam.goal=1e-5;p=[-1-122;0505];t=[-1-111];net=train(net,p,t);TRAINGDM,Epoch0/300,MSE3.6913/1e-05,Gradient4.54729/1e-10TRAINGDM,Epoch50/300,MSE0.00532188/1e-05,Gradient0.213222/1e-10TRAINGDM,Epoch100/300,MSE6.34868e-05/1e-05,Gradient0.0409749/1e-10TRAINGDM,Epoch114/300,MSE9.06235e-06/1e-05,Gradient0.00908756/1e-10TRAINGDM,Performancegoalmet.a=sim(net,p)a=-1.0026-1.00440.99690.99923.1MATLAB神经网路工具箱的GUI(图形用户界面)工具.神经网路工具箱的GUI工具主要包括:1)神经网路GUI工具主窗口;2)神经网路的构建窗口;3)网路训练对话框;4)自适应参数设置对话框;5)残差显示窗口.通过神经网路工具箱的GUI工具按键才能很便捷地打开所构建的神经网路的结布光进行察看,也可以看见一个训练过程的误差曲线变化图.3.2神经网路工具箱解决问题的通常步骤1)对待解决的问题进行剖析,按照各类网路的特征选用合适的网路模型;2)构建网路;3)对网路初始化;4)对网路进行训练;5)对网路进行仿真检验;6)应用网路解决问题.4系统的预测仿真4.1使用神经网路GUI工具构建神经网路的输入样本和目标样本1)在MATLAB命令窗口输入nntool,打开图形用户界面工具主窗口用matlab编bp神经网络预测程序,如图1所示.2)单击NewData按键,打开数据生成对话框.构建输入样本P,数据的输入和设置如图2所示,单击Create按键关掉对话框.3)根据上一步,输入目标样本T,数据类型选Targets.回到GUI工具的主窗口,单击Export按键弹出导入对话框,选中变量P和T,之后单击Export按键,把变量P和T导入到工作区.这为仿真文件从工作空间调用导出数据做好了打算.4.2构建仿真模型文件进行预测运行MATLAB软件中的Simulink仿真环境,在神经网路模块库中调用神经网路预测控制模块NNPredictiveController用matlab编bp神经网络预测程序,用模块封装技术构建湖泊水合数学多项式模块,联接讯号源模块和示波器模块后就完善了湖泊水质预测仿真文件predwq.mdl,如图3,其中FromWorkspace模块中是目标样本T的数据,可以直接从工作区导出.双击神经网路预测控制模块NNPredictiveController,弹出如图4的窗口,此窗口用于设计模型预测控制器,输入控制器变量空间N2和Nu、权值参数ρ和控制最优化参数α的值.之后点击PlantIdentification按键,打开系统识别窗口,从工作区导出输入样本P,设置好其它参数后训练网路,单击OK按键,将训练好的神经网路模型导出到神经网路预测控制模块中,在NNPredictiveController窗口上单击OK按键,将控制器参数导出到NNPredictiveController模块中.图3predwq.mdl仿真文件图4神经网路预测控制模块窗口系统模块SystemModel是用模块封装技术封装的湖泊水质微分方程式(4)的仿真模块,如图5所示.在predwqSimulink主窗口,仿真时间输入100,再单击Startsimulation命令按键开始仿真.仿真结束后,双击示波器模块就可以查看仿真结果,如图6所示.对仿真结果和目标样本的值进行比较,按照它们的差值绘出预测偏差变化曲线,如图7所示.图5湖泊水质微分等式仿真模块图6目标和预测结果图5结果与讨论比较图6、图7知,本文构建的网路系统对水质参数耗氧量的预测图象和目标样本基本一致.把仿真预测结果数据和实际目标样本数据进行比较,正、负最大偏差分别为0.11和-0.06,最小偏差为0,即使还有误差,但偏差是在满意的范围之内.为此,把湖泊水质的物理模型用MATLAB神经网路进行仿真预测,具有较高的精度,为湖泊水质预测提供了便捷的方式.图7预测偏差的曲线变化借助NNToolbox4.0.2构架神经网路主要采用以下两种方式:(1)使用网路数据管理器(NetworkDataManager)。
具击剑作为:在LaunchPad窗体中点击NeuralNetworkToolbox目录下的。nntool文件,即在计算机屏幕中央出现NetworkDataManager窗体;点击窗体中NewNetwork按键,按照提示设定网路类型、网络结构、网络算法和网路激活函数即可生成用户定义的神经网路;点击View按键可显示该神经网路的结布光;点击initialize、simu-late、train和adapt按键并设定参数可对神经网路进行初始化、模拟、训练和仿真;最后点击Export按键可将网路模拟、训练和仿真的结果以文件的方式导入。该方式操作简易,无需编撰程序代码,即可完成神经网路的建立、初始化、训练和仿真等主要工作。并且该方式不能和MATLAB其他程序动态链接,网路仿真结果只能以数据文件的方式导入,不能可视化显示。(2)编撰MATLAB应用程序,即运用MATLAB语言引用神经网路工具箱函数编撰程序代码并保存为M文件,之后运行该文件。该种方式可以依据研究人员的须要,调用MATLAB丰富的内部函数,并能和各种数据库及其他应用程序(包括C、FOR-TRAN程序)动态链接,使神经网路功能更为强悍。
本研究即采用该种方式,其中引用的重要算法、函数及参数将在第2、3节简述。中国未来几年人口总数的预测本文对所使用的序列数据进行GM(1,1)模型维数优化时得到最佳的维数是5~8维不等,均属于短序列预测,只适宜短期的人口总数的预测,所以对2008-2012年共5个时间序列点的中国人口总数进行预测,结果如表2所示。表2红色人工神经网路(GANN)模型对2008-2012年中国人口总数预测的结果千人年份20082009201020112012总人口132663132963133706134373135025构建BP神经网路预测模型在进行BP网路预测模型设计时,主要考虑网路的层数和每层中神经元的个数。神经网路通过计算机程序实现对非线性映射迫近,在诸多语言中,MATLAB语言容许物理方式的语言编撰程序,比其他语言更接近我们书写估算公式的思维方法。因而编程效率高,易学易懂。年份人口总量(千人)198510585119861075071987109300198811102619891127041990114333199111582319921171711993118517199411985019951211211996122389199712362619981247611999125786200012674320011276272002128453200312922720041299882005130756采用单隐层的BP网路进行预测[3]。
构建两层神经网路,因为输入样本为3维的输入向量,因而,输入层一共有3个神经元,按照Kolmogorov[2]定律,网路应当为3×7×3的结构。其中,threshold设定了网路输入向量的取值范围[0,1],第一层神经元数为3,传函类型为‘LOGSIG’,第二层神经元数为7,传函类型为‘PURELIN’,采用动量梯度增长反向传播算法对网路进行训练。中间层的神经元个数是很难确定的,而这又在很大程度上影响着网路的预测性能。当网路的预测偏差最小时,网路中间层的神经元数量就是最佳值。进行对比后,可见中间层神经元个数为8时,网路的预测性能最好。训练结果如图1所示,网路的预报偏差如Performanceis9.89455e-005,Goalis0.00010100.035-1100.030.025-2100.020.015-3100.010.005-4100-0.005050100150155Epochs-0.0111.21.41.61.822.22.42.62.83图1训练结果(中间层神经元数量:8)图2网路的预报偏差(中间层神经元数量:8)年份总人口数(千人)200614080020071425002008146600200915100020101558002011159600201216210020131633002014163800201516400020161641002017164100201816410020191641002020164100,每行句子前都有一个符号“>>”,此即命令提示符。
在此符号后(也只能在此符号后)输入各类句子并按Enter键,方可被MATLAB接收和执行。执行的结果一般就直接显示在句子下方,如图1.2所示。不同类型句子用不同颜色分辨。在默认情况下,输入的命令、函数、表达式以及估算结果等采用红色字体,字符串采用赭褐色,if、for等关键词采用红色,注释句子用红色。由于MATLAB是一个多功能集成软件,不同的功能须要使用不同的文件格式去表现,所以MATLAB的文件也有多种格式。最基本的是M文件、数据文件和图形文件,除此之外,还有MEX文件、模型文件和仿真文件等。下边分别给以说明。(1)M文件,以.m为扩充名,所以称为M文件。M文件是由一系列MATLAB句子组成的文件,包括命令文件和函数文件两类,命令文件类似于其他中级语言中的主程序或主函数,而函数文件则类似于子程序或被调函数。MATLAB诸多工具箱中的(函数)文件基本上是M函数文件。由于它们是由ASCII码表示的文件,所以可由任一文字处理软件编辑后以文本格式储存。(2)数据文件,以.mat为扩充名,所以又称MAT文件。在讨论工作空间窗口时早已涉及到MAT文件。其实,数据文件保存了MATLAB工作空间窗口中变量的数据。
(3)图形文件,以.fig为扩充名。主要由MATLAB的绘图命令形成,其实也可用File菜单中的New命令构建。(4)MEX文件,以.mex或.dll为扩充名,所以称MEX文件。MEX实际是由MATLABExecutable简写而成的,由此可见,MEX文件是MATLAB的可执行文件。(5)模型和仿真文件,模型文件以.mdl为扩充名,由Simulink仿真工具箱在构建各类仿真模型时形成。仿真文件以.s为扩充名。鼠标输入句子(input)其调用格式有(1)x=input('prompt'):显示提示字符串'prompt',要求用户鼠标输入x的值。(2)x=input('prompt','s'):显示提示字符串'prompt',要求用户鼠标输入字符型变量x的值,不至于将输入的数字看成是数值型数据。6.3.2屏幕输出句子(disp)屏幕输出最简单的方式是直接写出欲输出的变量或链表名,前面不加分号。据悉,可以采用disp句子,其调用格式为disp(x)。6.3.3M数据文件的储存/加载(save/load)1.save句子其调用格式有(1)save:将所有工作空间变量储存在名为MATLAB.mat的文件中。
(2)savefilename:将所有工作空间变量储存在名为filename的文件中。(3)savefilenameXYZ:将工作空间的指定变量X、Y、Z存于名为filename的文件中。2.load句子其调用格式有(1)load:假如MATLAB.mat文件存在,则加载MATLAB.mat文件中储存的所有变量到工作空间;否则返回一错误信息。(2)loadfilename:假如filename文件存在,则加载filename文件中储存的所有变量到工作空间;否则返回一错误信息。(3)loadfilenameXYZ:假如filename文件及储存的变量X、Y、Z存在,则加载filename文件中储存的变量X、Y、Z到工作空间;否则返回一错误信息。在MATLAB中,主要的二维绘图函数如下:(1)plot:x轴和y轴均为线性刻度。(2)loglog:x轴和y轴均为对数刻度。(3)semilogx:x轴为对数刻度,y轴为线性刻度。(4)semilogy:x轴为线性刻度,y轴为对数刻度。(5)plotyy:勾画双纵座标图形。其中plot是最基本的二维绘图函数,其调用格式有①plot(Y):若Y为实向量,则以该向量元素的下标为横座标,以Y的各元素值为纵座标,勾画二维曲线;若Y为复数向量,则等效于plot(real(Y),imag(Y));若Y为实矩阵,则按列勾画每列元素值相对其下标的二维曲线,曲线的条数等于Y的列数;若Y为复数矩阵,则按列分别以元素实部和虚部为横、纵座标勾画多条二维曲线。
②plot(X,Y):若X、Y为宽度相等的向量,则勾画以X和Y为横、纵坐标的二维曲线;若X为向量,Y是有一维与Y同维的矩阵,则以X为横座标勾画出多条不同色调的曲线,曲线的条数与Y的另一维相同;若X、Y为同维矩阵,则勾画以X和Y对应的列元素为横、纵坐标的多条二维曲线,曲线的条数与矩阵的列数相同。③plot(X1,Y1,X2,Y2,…Xn,Yn):其中的每一对参数Xi和Yi(i=1,2,...,n)的取值和所绘图形与②中相同。④plot(X1,Y1,LineSpec,...):以LineSpec指定的属性,勾画所有Xn、Yn对应的曲线。⑤plot(...,'PropertyName',PropertyValue,...):对于由plot勾画的所有曲线,根据设置的属性值进行勾画,PropertyName为属性名,PropertyValue为对应的属性值。⑥h=plot(...):调用函数plot时,同时返回每条曲线的图形句柄h(列向量)。①在工作空间查看各个变量,或在命令窗口用who,whos(注意大小写)查看各个变量。②在工作空间双击变量,弹出ArrayEditor窗口(链表编辑器窗口),即可更改变量。
③使用save命令把工作空间的全部变量保存为my_var.mat文件。>>savemy_var.mat④输入下述命令:>>clearall%消除工作空间的所有变量观察工作空间的变量是否被清空。使用load命令把刚刚保存的变量载入工作空间。>>loadmy_var.mat⑤清除命令窗口命令:>>clc(本资料素材和资料部份来自网路,仅供参考。请预览后才下载,期盼您的好评与关注!)Training-BlueGoal-BlackPAGE/NUMPAGES









