人工神经网路,简称神经网路,是一种模仿生物神经网路的结构和功能的物理模型或则估算模型。似乎是一种与贝叶斯网路很像的一种算法。之前看过一些内容仍然云里雾里,此次决定写一篇博客。搞清这个基本原理,虽然现今深度学习太火了。
神经网路是一种方式,既可以拿来做有监督的任务,如分类、视觉辨识等,也可以用作无监督的任务。首先,我们看一个简单的反例。如右图所示(这个图网上有好多人引用了,但我找不到出处,欢迎见谅),假如我们想训练一个算法可以使其辨识出是猫还是狗,这是很简单的一个分类任务,我们可以找一条线(模型),在这个二元座标中进行“一刀切”,把这两组数据分开。我们晓得,在解析几何中,这条直线可以用如下的公式抒发:
#8:0:6:c:0:6:6:2:e:7:e:0:3:7:c:2:6:e:3:4:d:2:e:c:f:b:b:1:f:c:a:4#
图1猫狗数据
#e:6:8:a:a:3:2:8:f:d:1:d:8:7:a:9:4:5:5:b:4:a:b:4:0:1:2:4:a:5:f:8#
图2一个简单的神经网路
这儿的W1和W2就是两个座标轴上的系数,可以称为权重。W0可以叫做截距,也称作偏斜。新来一个数据点,也就是一组输入值(X1,X2),假如在这条线的一侧,这么它就是一只狗,假如在左侧就是一只猫了。这就可以用一个简单的神经网路来表示。如图2所示,X1和X2分别是输入值,Y是输出值,两条边的权重分别是W1和W2。这是一个最简单的神经网路了。这就是使用神经网路定义了一个线性分类器了。这儿的一个矩形的节点就是一个神经元。我们也可以采用另一种方法,即在输入输出之间加一个中间节点S,之后降低一个输出层,包括两个节点Y1和Y2,分别对应猫和狗,最后那个输出节点的值大,这么这个数据就属于那个类别(猫或则狗)。
#2:f:e:1:f:c:1:4:e:7:8:f:1:e:0:b:0:b:b:1:1:6:a:8:c:d:6:c:5:6:7:6#
#c:2:5:d:1:c:3:6:8:e:b:7:6:7:8:1:2:2:e:5:c:e:c:5:d:4:7:d:1:a:a:d#
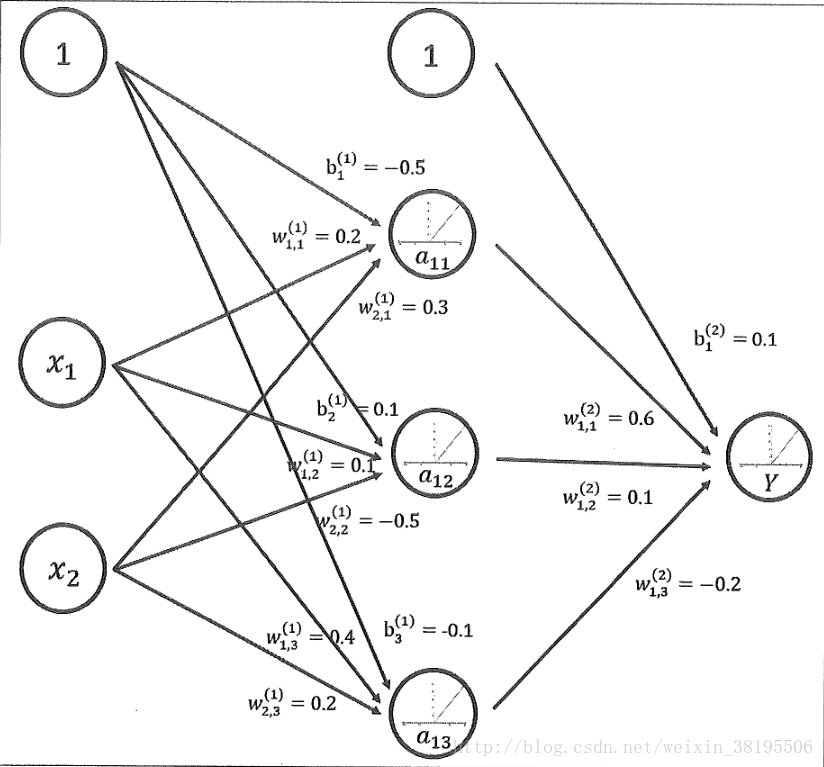
对于简单的二分类问题这就可以解决了。但在实际情况中,有好多问题未能简单的使用“一刀切”的形式解决,如图3所示,假定猫和狗的数据分布如右图,这么这就难以用“一刀切”的形式来解决了,并且我们可以切两刀,横竖各一刀,之后把相同的“块”联合上去,这样就解决了比较复杂的分类问题了。也有些问题,须要用曲线来分割。在这些情况下,我们就须要比较复杂一点的神经网路了。以曲线为例,我们可以设计出一个三层的神经网路。这就是用神经网路设计的一个非线性分类器。理论上讲,怎么一个分类器都可以设计一个神经网路来表征,也就是说,不管实际图形怎样,我们都可以设计一个神经网路来拟合。到这儿,可能有人问,每位节点的这个函数要怎么选择?按照吴军老师《数学之美》第二版中的说法,为了提供人工神经网路的通用性,我们通常规定每位神经元的函数只能针对其输入的变量做一次非线性的变换。举个反例说就是如果某个神经元Y的输入值是X1,X2,...Xn,它们的边的权重分别为W1,W2,...Wn,这么估算Y节点的值分两步进行,第一步是估算来自输入值的线性组合:
第二步是估算y=f(G),这儿的f(⋅)可以使非线性的,,但由于上面的参数是一个具体的值,所以不会很复杂。这两个步骤的结合促使人工神经网路既灵活又不至于太复杂。这儿的f(⋅)就是激活函数。线性模型的抒发能力不够,它的作用就是来提高模型的表示能力。人工神经网路可以好多层联接在一起,因而在人工神经网路中,主要的工作就是设计结构(基层网路,每层几个节点等)和激活函数。我们常用的激活函数包括Sigmoid函数、ReLU函数、Tanh函数等等。如右图所示,这是几种简单的激活函数的示意图
#a:0:3:9:f:2:c:5:2:3:d:6:7:8:2:a:2:4:8:9:a:3:2:b:9:2:b:7:4:c:1:3#









