这是2021年江苏省南京市高考语文的一道作图题,要求过圆外一点作已知圆的一条切线。相信好多考生都只会用一种方式来画图吧。老黄看过他人的答案,不知道是不是标准答案,他倒是用了两种方式,不过虽然第二种方式只是在上面一小部份取了一下巧,并没有真正做到,用两种不同的方式来解决。先瞧瞧原题:
如图,已知P是⊙O外一点,用两种不同的方式过点P作⊙O的一条切线. 要求:
(1)用尺子和圆规画图;
(2)保留画图的痕迹,写出必要的文字说明.
分析:(1)①正常的情况应当能想到借助“直径对直角”的定律来解决这个问题。
因为过半径端点,且与半径相互垂直的直线,是圆的切线。这是切线的通常判断定律,所以很容易想到,通过过P的直线与直径所产生的直角,使直角顶点在圆上,那么这条过P的直线,就是所求。而由“直径对直角”,就可以晓得,这个直角应当是以OP为半径的圆的圆周角。这样就得到了一种画图的方式。
②当然方式还有好多,但老黄这儿要用的是切割线的定律的灵活应用的技巧。由切割线定理,过P点的切线长的平方等于过P点的割线与圆的两个交点到P点的距离的积。也可以解决这个问题。切割线定律如今早已被删掉出教材了。但建议中学生还是要通过自学把它把握上去的,因为它很有可能在高考中,可以起到大作用。具体的画图方式,看下边的解题过程。
(2)因为这道题是有要求写作法的。现在课堂上,对于画图的文字说明,都没有硬性要求,遇到这样的题目,估计好多考生都不知道究竟应当如何写文字说明吧。下面老黄就给你们做一个演示。
解:(方法1)如图1:
①联结OP,取OP的中点M.
②以M为圆心,OM为直径作弧,交⊙O于N,
③连接PN,PN就是⊙O的切线.【上面提及他人用的第二种方式,是取PO中点这一步,用做PO为底的等边三角形,再做PO上的高,利用“等腰三角形斜边三线合一”的定律,取PO的中点,来取巧。 这个方式虽然并不符合题目要求!因为这样做是用两种不同的方式取OP的中点,而不是用两种不同的方式作圆的切线】
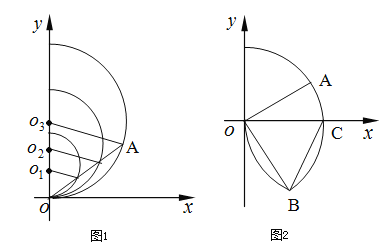
(方法2)如图2:
①联结OP交⊙O于点A,并延长交⊙O于点B,
②取PB的中点C,以C为圆心,BC为直径作⊙C.
③过A作⊙O的切线交⊙C于点D
④以P为圆心,PD为直径,作弧交⊙O于点E,
⑤连接PE,PE就是⊙O的切线.
再指出一下,方法1应用的是“直径对直角”;方法2应用的是“切割线定理”。您都把握了吗?









