在深度学习中,我们常常用到损失函数,损失函数选择使用情况直接决定我们模型训练疗效。在pytorch深度学习中存在好多种损失函数。主要分为19种。
1、均方误差损失 MSELoss
2、交叉熵损失 CrossEntropyLoss
3、KL 散度损失 KLDivLoss
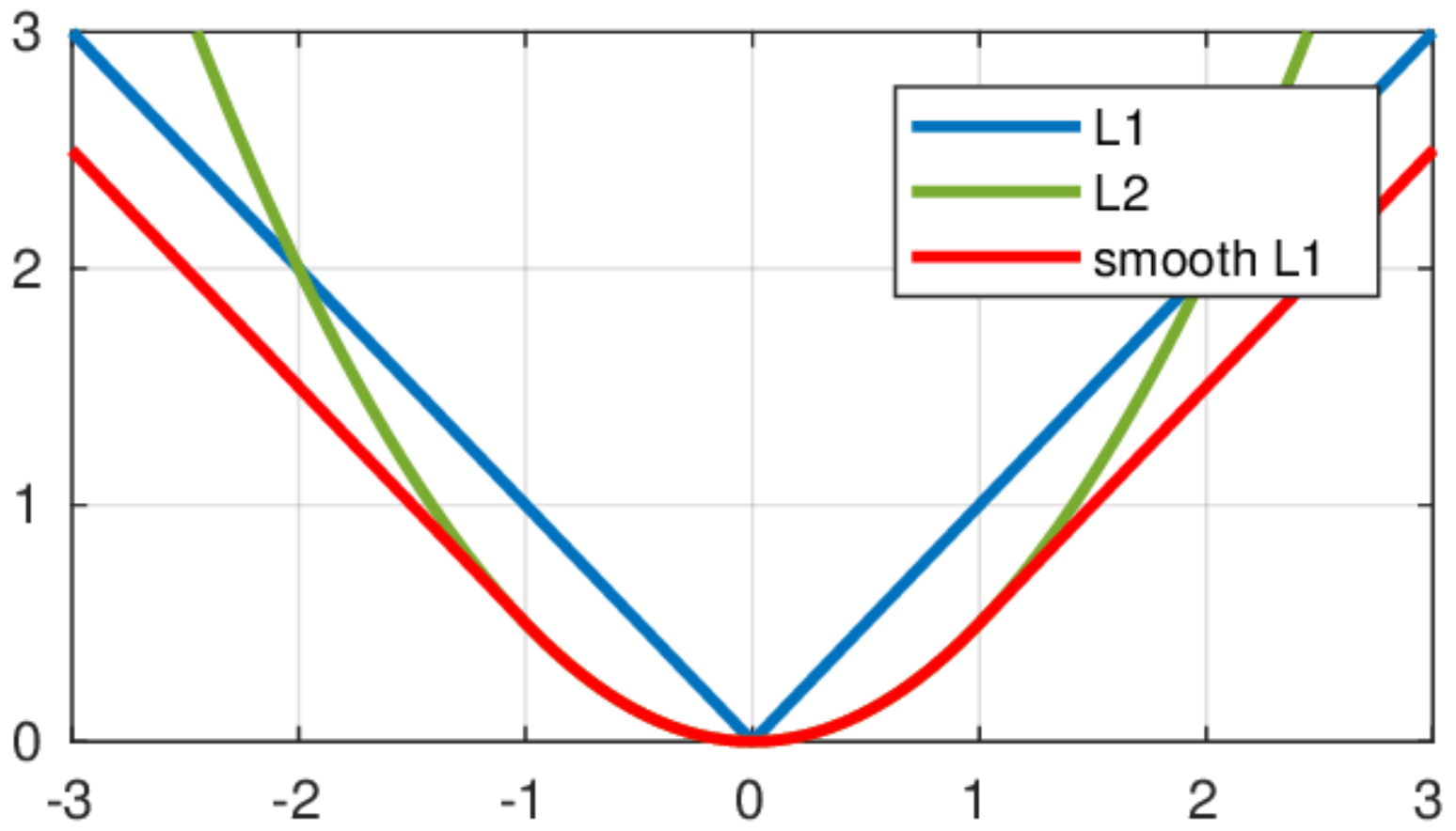
4、L1范数损失(L1_loss)
5、L2范数损失(L2_loss)
6、平滑版L1损失 SmoothL1Loss
7、二进制交叉熵损失 BCELoss
8、BCEWithLogitsLoss
9、HingeEmbeddingLoss
10、2分类的logistic损失 SoftMarginLoss
11、多标签分类损失 MultiLabelMarginLoss
12、多标签 one-versus-all 损失 MultiLabelSoftMarginLoss
13、cosine 损失 CosineEmbeddingLoss
14、多类别分类的hinge损失 MultiMarginLoss
15、三元组损失 TripletMarginLoss
16、连接时序分类损失 CTCLoss
17、负对数残差损失 NLLLoss
18、NLLLoss2d
19、PoissonNLLLoss
8、MarginRankingLoss
下面将依照次序进行损失函数介绍。
1.前言
损失函数是深度学习与机器学习上面的重要函数。从字面意思可确定,损失函数(Loss Function)反应的是模型对数据的拟合程度。损失函数越小,说明模型对数据拟合程度越好,反之拟合程度越差。
损失函数是拿来估量模型的预测值prediction(x)与真值Y之间的不一致问题,非负值函数,通常L(Y,prediction(x))表示损失函数公式,损失函数越好,鲁棒性越好,损失函数是经验风险函数的核心部份,也是结构风险函数的重要组成部份。模型的结构风险函数包括了经验风险项和正则项,通常可以表示成如下多项式:
其中,前面的均值函数表示的是经验风险损失函数,L表示的是损失函数,后面的是正则化项。
本文主要搜集和整理了深度学习常用的损失函数,给出函数抒发方式,以及使用介绍和应用场景。
2.常用损失函数
**2.1 均残差函数(MSE)
概念:均方差损失函数是预测值和原始数据对应点偏差的平方和的均值,
公式:
N个样本数。
pytorch中实例演示:
代码:
import torch
import torchvision
from torch import nn
input=torch.rand(1,5,requires_grad=True)
target=torch.rand(1,5)
loss=torch.nn.MSELoss()
output=loss(input,target)
结果:在这儿插入代码片
input: tensor([[0.5939, 0.8272, 0.7765, 0.7223, 0.5796]], requires_grad=True)
target: tensor([[0.7467, 0.0961, 0.0630, 0.3596, 0.3448]])
output: tensor(0.2507, grad_fn=<MseLossBackward>)
#运行结果为0.2507,
上面展示在torch中调用算法演示,下面讲解一下内部运行机制。
代码:
input=[0.5939, 0.8272, 0.7765, 0.7223, 0.5796]
target=[0.7467, 0.0961, 0.0630, 0.3596, 0.3448]
input=torch.tensor(input)
target=torch.tensor(target)
result=(input-target)**2
output=result.view(5,).sum()/5
print("result:",result)
print("output:",output)
结果:
result: tensor([0.0233, 0.5345, 0.5091, 0.1316, 0.0551])
output: tensor(0.2507)
计算结果与torch.nn.MSELoss()相同,为0.2507
2.2 交叉熵损失(CrossEntropyLoss)
**概念:**交叉熵是信息论中的一个重要概念,主要用于测度两个机率分布间的差异性,要理解交叉熵,需要先了解下边几个概念。
信息量:****信息量拿来去除随机不确定的东西,衡量信息量的大小就是看这个信息去除不确定性的程度。
这一个损失函数在深度学习中常常使用,我们重点讲解。
例如:“地球是圆的”,这是确定的信息,这句话并没有降低不确定性,信息量为0.
根据上述可总结如下,信息量的大小与信息发生的机率生正比。概率越大,信息量越小。概率越小,信息量越大。
设某一风波发生的机率为P(x),其信息量表示为:
其I(x)表示信息量大白话讲解机器学习-损失函数,这里log表示e为底的自然对数。
信息熵:信息熵被称为熵,用来表示所有信息量的期望。
期望是试验中每次可能结果的机率除以其结果的总和。
所以信息量的熵可表示为:(这里的X是一个离散型随机变量)
举一个抓球的事例大白话讲解机器学习-损失函数,箱子中有黑色球5个,绿色求3个,蓝色球2个。则从袋子中随机抓取一个球,计算信息熵。
对于0-1分布的问题,由于其结果只用两种情况,是或不是,设某一件事情发生的机率为 P ( x ),则另一件事情发生的机率为 1 P ( x ) ,所以对于0-1分布的问题,计算熵的公式可以简化如下:
2.3 相对熵(KL散度)
如果对于同一个随机变量 X X X有两个单独的机率分布 P ( x ) 和 Q ( x ) ,则我们可以使用KL散度来评判这两个机率分布之间的差别。
下面直接列举公式,再举例子加以说明。
在机器学习中,常常使用 P(x)来表示样本的真实分布, Q ( x )来表示模型所预测的分布,比如在一个三分类任务中(例如,猫狗马分类器), x 1 , x 2 , x 3 分别代表猫,狗,马,例如一张猫的图片真实分布 P ( X ) = [ 1 , 0 , 0 ] , 预测分布 Q ( X ) = [ 0.7 , 0.2 , 0.1 ] ,计算KL散度:
KL散度越小,表示 P ( x ) 与 Q ( x ) 的分布愈加接近,可以通过反复训练 Q ( x ) 来使 Q ( x ) 的分布迫近 P ( x ) 。
交叉熵
首先将KL散度公式拆开:
前者 H ( p ( x ) ) 表示信息熵,后者即为交叉熵,KL散度 = 交叉熵 - 信息熵
交叉熵公式表示为:
在深度学习训练网路时,输入数据与标签时常早已确定,那么真实机率分布 P ( x ) 也就确定出来了,所以信息熵在这儿就是一个常量。由于KL散度的值表示真实机率分布 P ( x ) 与预测机率分布 Q ( x ) 之间的差别,值越小表示预测的结果越好,所以须要最小化KL散度,而交叉熵等于KL散度加上一个常量(信息熵),且公式相比KL散度愈发容易估算,所以在深度学习中经常使用交叉熵损失函数来估算loss就行了。
在线性回归问题中,常常使用MSE(Mean Squared Error)作为loss函数,而在分类问题中经常使用交叉熵作为loss函数。
下面通过一个事例来说明怎样估算交叉熵损失值。
假设我们输入一张狗的图片,标签与预测值如下:
那么loss:
loss=(0log(0.2)+1log(0.7)+0log(0.1))=0.36
一个batch的loss为:
m表示样本数。
代码:
import torch
import torchvision
from torch import nn
from torch.nn.functional import cross_entropy
import random
import numpy as np
p=torch.randn([2,3])
t=torch.tensor([2,1])
print(p)
print(t)
p=torch.softmax(p,dim=-1)
print("p:",p)
gold_probs=torch.gather(p,1,t.unsqueeze(1)).squeeze()
print("gold_probs:",gold_probs)
step_loss=torch.mean(-torch.log(gold_probs))
print("loss2:",step_loss)
结果:
tensor([[ 3.4984, -0.1238, 2.7632],
[-1.0089, -1.7351, 0.6044]])
tensor([2, 1])
p: tensor([[0.6640, 0.0177, 0.3183],
[0.1538, 0.0744, 0.7718]])
gold_probs: tensor([0.3183, 0.0744])
loss2: tensor(1.8716)
总结:
交叉熵才能评判同一个随机变量中的两个不同机率分布的差别程度,在机器学习中就表示为真实机率分布与预测机率分布之间的差别。交叉熵的值越小,模型预测疗效就越好。
交叉熵在分类问题中经常与softmax是标配,softmax将输出的结果进行处理,使其多个分类的预测值和为1,再通过交叉熵来估算损失。
END:本章节主要讲解均方差与交叉熵损失函数,其他损失函数后章节介绍。









