本篇博客主要是基于花书(古德费洛的《DeepLearning》)和香蕉书(周志华的《机器学习》)撰写的,其中插入了博主的一些个人看法,如有不对之处希望你们强调来一上去讨论一下嘿嘿,万分谢谢。
哪些是一个好的机器学习算法?
我想我们可以先从这个问题开始:一个机器学习算法满足哪些条件才会被称得上是一个好算法?
机器学习的主要挑战是我们的算法必须才能在当初未观测到的新输入上表现良好,而不只是在训练集上表现良好。这个很容易理解,由于我们平常里所做的就是给一个机器学习算法喂一大堆数据(训练集),之后希望这个算法在新数据(测试集)上有良好的性能。而这些在以前未观测到的输入上表现良好的能力被称为泛化能力。
为了得到泛化能力好的学习器,我们应当从训练样本中尽可能学出适用于所有潜在样本的“普遍规律”,这样就能在遇见新样本时作出正确的判断。假如我们把训练样本的一些特有的特性也当作潜在样本的通常性质,这样才会造成泛化能力下滑,这也是我们常说的“过拟合”现象。
与“过拟合”相对的是“欠拟合”,即训练样本的性质都没有学习完全,这样又如何能指望对未知的新样本表现良好呢?举个事例,例如现今要辨识猫和狗。猫和狗都有两个耳朵,有双脚,有尾巴,有胡须,假如我们学习器学习能力不行,只学习到了那些比较“浅”的特点,这么这个学习器肯定都未能对训练集图片进行正确的分类,这就是欠拟合。假如学习器除了学习到了这种特点,还学习到了猫和狗有不同的身材、体态、眼睛形状等合理的特点,这么我们除了在训练集上分类偏差很低,在测试集上也能达到不错的疗效,这是学习器成功的反例。假如再进一步,学习器在之前的基础上,还学到了好多何必要的特点,例如训练集中有的狗少了一只腿,或则红色头发的狗比较多,这么学习器很有可能将一只少了一条腿的猫分类到狗的类别,或则觉得其他颜色头发的狗是狗的机率很低。这种特点强烈干扰了学习器的正确判定,这便是“过拟合”。
总结一下,决定机器学习算法疗效是否好有如下两个诱因:
(1)增加训练偏差
(2)缩小训练偏差和测试偏差的差别
这两个诱因分别对应机器学习的两个挑战:欠拟合和过拟合。欠拟合是指模型不能在训练集上获得足够低的偏差,而过拟合是指训练偏差和测试偏差之间的差别太大。
独立同分布假定
里面提及我们希望尽可能最小化模型的泛化偏差,这么泛化偏差应当怎样评判呢?一般我们是通过测度在训练集中界定下来的测试集样本上的性能,来近似恐怕模型的泛化偏差。但归根究竟,测试集也是我们“能观测到的已有的数据”的一部份,用它来代表剩下的未观察到的潜在数据还是具有太大的局限性。不过,我们也不能为了辨识猫狗,就把世界上所有的猫狗相片全部找过来,我们就能分别猫狗,但我们也没有见过世界上所有的猫狗,不是吗?
对于这个问题统计学理论提供了一些答案。现今不妨换个角度思索,假定我们如今得到了世界上所有的猫狗相片的数据,并且由于太多,我们还是不想全部使用,于是我们根据一定规律从中抽取一些数据,保证这种数据包含所有的必要特点,才能100%代表整体数据。在这样的假定下,训练集偏差、测试集偏差以及剩下所有数据的偏差理论上应当都一样,这不正是我们想要的疗效?
如今将前面的大白话说的更理论化一些。训练集和测试集数据通过数据集上被称为数据生成过程的机率分布生成,我们假定每位数据集中的样本都彼此互相独立,但是训练集和测试集都是同分布的,取样自相同的分布,我们将这个共享的潜在分布称为数据生成分布,记为pdatapdata。这就是独立同分布假定,这促使我们能否用单个样本的机率分布叙述数据生成过程。
在独立同分布的假定下,训练样本的偏差就等价于潜在样本的偏差,我们只要尽可能减少训练偏差即可。但实际上这个假定基本不能能组建,我们常常只是借助部份数据预测整个数据分布,从这个角度来说“过拟合”是难以彻底杜绝的,我们所能做只是减轻或则降低其风险。辛运的是,但这并不影响我们使用这个假定,大多数情况下算法还是能得到比较令人满意的结果,但是我们还可以使用其他方法进一步提高结果。
模型容量与过拟合
如今再从模型容量的角度谈一谈过拟合。
模型的容量是指其拟合各类函数的能力。我们可以将一个模型视为一个复杂的函数f(X)=Yf(X)=Y,给定输入XX,之后才能得到相应的输出Y"role="presentation">YY。这个函数参数越多,函数就越复杂,才能拟合的函数也就越多越中级。其实,影响模型容量的不止是参数数目,训练目标也能影响。训练模型的目的就是从这种函数中选购出最优函数,但是实际中算法不会真的找到最优函数,而仅是找到一个可以大大减少训练偏差的函数。一些额外的限制诱因,例如优化算法的不完美,会造成算法容量减少。
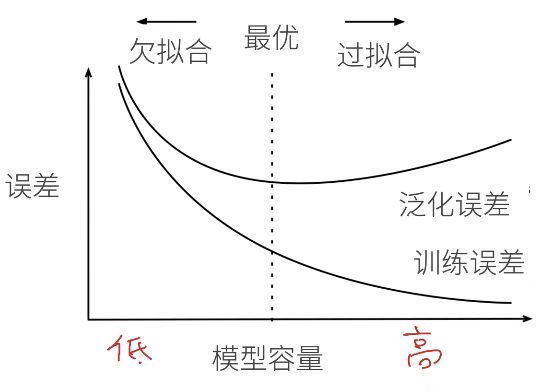
通过调整模型的容量,我们可以控制模型是否偏向于过拟合或欠拟合。当机器学习算法的容量适宜于所执行任务的复杂度和所提供训练数据的数目时,算法疗效一般会最佳。容量不足的模型不能解决复杂任务;容量高的模型还能解决复杂的任务,并且当其容量低于任务所需时,有可能会发成生拟合。如右图所示。
我们比较了线性、二次和9次函数拟合真实二次函数的疗效。线性函数未能描画真实函数的曲率,所以欠拟合。9次函数就能表示正确的函数,但由于训练参数比样本还多,所以它也能表示无限多个正好穿过训练样本点的其他函数,我们很难从那些不同解中选出一个泛化良好的。二次模型十分符合任务的真实结构,因而它可以挺好地泛化到新数据上。
上图是容量和偏差之间的典型关系。在达到最优容量前,训练偏差和泛化偏差都很高(容量不够时,最优函数可能没有包括在模型还能拟合的函数族中)。假如继续降低容量,训练偏差减少,而且训练偏差和泛化偏差的宽度不断扩大,最终这个宽度超过训练偏差的增长,步入到过拟合机制。为此我们不能为了增加训练偏差一味增强模型容量,要针对具体问题选择合适的模型容量。
最后再来看看训练样本数目对模型有哪些影响。
举个板栗,通过给一个5阶方程添加适当的噪音,构造一个回归问题,之后用二次模型和最优容量的模型去求解该问题,如上图所示。图中红色的实线是贝叶斯偏差,即从预先晓得的真实分布预测而出现的偏差,也是理论上能达到的最佳偏差。例如说,一个色子,理论上6个面出现的概率都是1616,但假如我们实际扔6次,并不能保证每位面各出现一次,这个偏差就称作贝叶斯偏差(也可以理解为系统固有偏差?)。其实一个算法由于各类各样的诱因肯定会有偏差,而贝叶斯偏差就是一个算法能达到的最优偏差。
对于二次模型,当训练样本数目还不足以匹配其模型容量时,训练偏差会随着样本的降低而增加,但若果继续降低训练样本,超过了模型的拟合能力,训练偏差(图中红色的线)会开始上升。而测试偏差会急剧减少,这是由于训练数据越多,关于训练数据的不正确的假定就越少。因为二次模型的容量不足以解决该问题,所以测试偏差会稳定在一个较高的水平。
对于最优容量的模型,测试偏差最终会趋近于贝叶斯偏差。训练集偏差可以高于贝叶斯偏差,由于该模型有能力记住训练集中的样本。但当训练集趋向无穷大时,任何固定容量的模型的训练偏差都起码增至贝叶斯偏差。
有心的人可能会问机器学习防止过拟合,偏差既能被模型容量影响又能被样本数目影响,这么我们该怎么针对某个容量的模型选择训练集大小,或则已有某个大小的训练集,怎么选择合适容量的模型呢?
从前面这张图解释了这个问题。可以听到机器学习防止过拟合,当训练集减小时,最优容量也会急剧减小,但当最优容量足够捕获模型复杂度以后就不再下降了。
到这儿可能还是有点绕,推论还没这么清晰。如今将两张图结合在一起看一下,如今我们假设要解决的问题的复杂度是固定的。当样本数目不够多时,训练集还不能挺好的反应真实的数据分布pdatapdata,即用小训练集学习到的只是全部数据的部份特点,每次降低训练集都引入了新的有用特点,模型发觉现有模型容量不足以学习,所以在早期模型的最优容量会随着训练集的减小而减小。假如训练集降低到一定地步,这时训练集早已足够反应真实数据分布了,再降低训练集只是相当于多了一些重复的样本,所以模型的最优容量不会再降低了。在这个降低训练集大小的过程中,假如在中途由于训练样本不够终止了,这个训练集大小对应的模型最优容量大于问题的复杂度,这么此时测试偏差都会过高,由于这个容量下难以捕获到真实数据分布的全部信息。
在实际应用中,我们一般是用有限的数据去预测真实分布。假如我们选择恰好和这个训练集大小相匹配的模型容量,常常测试偏差会偏低,由于此时的模型容量和问题复杂度不匹配。并且模型容量是一个很模糊的边界,很难确定一个深度学习算法的容量,所以一般我们会使用一个容量比训练集大好多的模型,来防止容量不够的问题,但这样岂不是会发生过拟合?是的,但通过正则化等方式我们可以减少过拟合带来的影响。正则化将在下一篇博客中讲。
总结
原本准备将过拟合和正则化放在同一篇博客里的,结果发觉过拟合讲了如此多(知识真是常读常新啊)。
回到题外话,在我看来,过拟合的假象是训练偏差很小,而测试偏差很大,给人一种模型“记住”样本的觉得,所以换个新样本就瓦特了。但归根究竟还是模型容量以及训练集这三者和问题复杂度是否匹配的问题。
假如模型容量过小,无论你给多少训练样本,都未能得到一个较低水平的泛化偏差,还有可能发生欠拟合;
假如模型容量超过问题的复杂度,但你给的训练样本不够(不是指数目,而是其包含的特点不够),模型很轻松能学习到训练集的特点,但泛化能力仍然很有限,这就造成了过拟合;
只有当模型容量和训练集大小这三者与问题复杂度平衡时,就能得到理想的泛化偏差。
不过现实中条件有限,难以获知数据的真实分布,所以一般使用大容量模型+正则化来得到不错的结果。









