《信号与线性系统剖析吴大正习题答案》由会员分享,可在线阅读,更多相关《信号与线性系统剖析吴大正习题答案(257页典藏版)》请在读根文库上搜索。
1、专业课习题解析课程第2讲第一章讯号与系统(二)1-1画出下述各讯号的波形【式中】为斜升函数。(2)(3)(4)(5)(7)(10)解:各讯号波形为(2)(3)(4)(5)(7)(10)1-2画出下述各讯号的波方式中为斜升函数。(1)(2)(5)(8)(11)(12)解:各讯号波形为(1)(2)(5)(8)(11)(12)1-3写出图1-3所示各波形的表达式。1-4写出图1-4所示各序列的闭合方式表达式。1-5判断下述各序列是否为周期性的。若果是,确定其周期。(2)(5)解:1-6已知讯号的波形如图1-5所示,画出下述各函数的波形。(1)
2、(2)(5)(6)(7)(8)解:各讯号波形为(1)(2)(5)(6)(7)(8)1-7已知序列的图形如图1-7所示,画出下述各序列的图形。(1)(2)(3)(4)(5)(6)解:1-9已知讯号的波形如图1-11所示,分别画出和的波形。解:由图1-11知,的波形如图1-12(a)所示(波形是由对的波形偏压为原先的两倍而得)。将的波形反转而得到的波形,如图1-12(b)所示。再将的波形右移3个单位,就得到了,如图1-12(c)所示。的波形如图1-12(d)所示。1-10估算下述各题。(1)(2)(5)(8)1-12如图1-13所示的电路,写出(
3、1)以为响应的微分等式。(2)以为响应的微分等式。1-20写出图1-18各系统的微分或差分多项式。1-23设系统的初始状态为,激励为,各系统的全响应与激励和初始状态的关系如下,试剖析各系统是否是线性的。(1)(2)(3)(4)(5)1-25设激励为,下述是各系统的零状态响应。判定各系统是否是线性的、时不变的、因果的、稳定的?(1)(2)(3)(4)(5)(6)(7)(8)1-28某一阶LTI离散系统,其初始状态为。已知当激励为时,其全响应为若初始状态不变,当激励为时,其全响应为若初始状态为,当激励为时,求其全响应。第二章2-1已知描述系统的微分等式和初始状态如下
4、,试求其零输入响应。(1)(4)2-2已知描述系统的微分等式和初始状态如下,试求其值和。(2)(4)解:2-4已知描述系统的微分等式和初始状态如下,试求其零输入响应、零状态响应和全响应。(2)解:2-8如图2-4所示的电路,若以为输入,为输出,试列举其微分等式,并求出冲激响应和前馈响应。2-12如图2-6所示的电路,以电容电流为响应,试求其冲激响应和前馈响应。2-16各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试求下述频域,并画出波形图。(1)(2)(3)(4)(5)波形图如图2-9(a)所示。波形图如图2-9(b)所示。波形
5、图如图2-9(c)所示。波形图如图2-9(d)所示。波形图如图2-9(e)所示。2-20已知,求2-22某LTI系统,其输入与输出的关系为求该系统的冲激响应。2-28如图2-19所示的系统,试求输入时,系统的零状态响应。2-29如图2-20所示的系统,它由几个子系统组合而成,各子系统的冲激响应分别为求复合系统的冲激响应。第三章习题3.1、试求序列的差分、和。3.6、求下述差分多项式所描述的LTI离散系统的零输入相应、零状态响应和全响应。1)3)5)3.8、求下述差分多项式所描述的离散系统的单位序列响应。2)5)3.9、求图所示各系统的单位序列响应。(a)(c)3.10、求
6、图所示系统的单位序列响应。3.11、各序列的图形如图所示,求下述频域和。(1)(2)(3)(4)3.13、求题3.9图所示各系统的前馈响应。3.14、求图所示系统的单位序列响应和前馈响应。3.15、若LTI离散系统的前馈响应,求其单位序列响应。3.16、如图所示系统,试求当激励分别为(1)(2)时的零状态响应。3.18、如图所示的离散系统由两个子系统级联组成,已知,激励,求该系统的零状态响应。(提示:借助频域和的结合律和交换律,可以简化运算。)3.22、如图所示的复合系统有三个子系统组成,它们的单位序列响应分别为,求复合系统的单位序列响应。第四章习题4.6求下述周期讯号的基波角频度和周期T
7、。(1)(2)(3)(4)(5)(6)4.7用直接估算傅里叶系数的方式,求图4-15所示周期函数的傅里叶系数(三角方式或指数方式)。图4-154.10借助奇偶性判定图4-18示各周期讯号的傅里叶系数中所富含的频度份量。图4-184-11某1内阻两端的电流如图4-19所示,(1)求的三角方式傅里叶系数。(2)借助(1)的结果和,求下述无穷级数之和(3)求1内阻上的平均功率和电流有效值。(4)借助(3)的结果求下述无穷级数之和图4-194.17依据傅里叶变换对称性求下述函数的傅里叶变换(1)(2)(3)4.18求下述讯号的傅里叶变换(1)(2)(3)(4)(5)4
8、.19试用频域微积分性质,求图4-23示讯号的频谱。图4-234.20若已知,试求下述函数的频谱:(1)(3)(5)(8)(9)4.21求下述函数的傅里叶变换(1)(3)(5)4.23试用下述方法求图4-25示讯号的频谱函数(1)借助延时和线性性质(门函数的频谱可借助已知结果)。(2)借助频域的积分定律。(3)将看作门函数与冲激函数、的频域之和。图4-254.25试求图4-27示周期讯号的频谱函数。图(b)中冲激函数的硬度均为1。图4-274.27如图4-29所示讯号的频谱为,求下述各值何必求出(1)(2)(3)图4-294.28借助能量方程估算下述积分的值
9、。(1)(2)4.29一周期为T的周期讯号,已知其指数方式的傅里叶系数为,求下述周期讯号的傅里叶系数(1)(2)(3)(4)4.31求图4-30示电路中,输出电流电路中,输出电流对输入电压的频度响应,为了能无失真的传输,试确定R1、R2的值。图4-304.33某LTI系统,其输入为,输出为式中a为常数,且已知,求该系统的频度响应。4.34某LTI系统的频度响应,若系统输入,求该系统的输出。4.35一理想低通混频器的频度响应4.36一个LTI系统的频度响应若输入,求该系统的输出。4.39如图4-35的系统,其输出是输入的平方,即(设为实函数)。该系统是线性的吗?(1
10、)如,求的频谱函数(或画出频谱图)。(2)如,求的频谱函数(或画出频谱图)。4.45如图4-42(a)的系统,带通混频器的频度响应如图(b)所示,其相频特点,若输入求输出讯号。图4-424.48有限频带讯号的最高频率为100Hz,若对下述讯号进行频域采样,求最小采样频度。(1)(2)(3)(4)4.50有限频带讯号,其中,求的冲激函数序列进行采样(请注意)。(1)画出及采样讯号在频度区间(-2kHz,2kHz)的频谱图。(2)若将采样讯号输入到截至频度,幅度为的理想低通混频器,即其频度响应画出混频器的输出讯号的频谱,并求出输出讯号。图4-47图4-48图4-494.53求
11、下列离散周期讯号的傅里叶系数。(2)第五章5-2求图5-1所示各讯号拉普拉斯变换,并标明收敛域。5-3借助常用函数(比如,等)的象函数及拉普拉斯变换的性质,求下述函数的拉普拉斯变换。(1)(3)(5)(7)(9)(11)(13)(15)1235-4如已知因果函数的象函数,求下述函数的象函数。(1)(4)5-6求下述象函数的原函数的终值和初值。(1)(2)5-7求图5-2所示在时接入的有始周期讯号的象函数。图5-25-8求下述各象函数的拉普拉斯变换。(1)(3)(5)(7)(9)5-9求下述象函数的拉普拉斯变换,并简略画出它们的波形图。
12、(1)(3)(6)其波形如右图所示:其波形如右图所示:其波形如右图所示:5-10下述象函数的原函数是接入的有始周期讯号,求周期T并写出其第一个周期()的时间函数表达式。(1)(2)5-12用拉普拉斯变换法解微分多项式的零输入响应和零状态响应。(1)已知。(2)已知。5-13描述某系统的输出和的联立微分多项式为(1)已知,求零状态响应,。5-15描述某LTI系统的微分多项式为求在下述条件下的零输入响应和零状态响应。(1)。(2)。5-16描述描述某LTI系统的微分多项式为求在下述条件下的零输入响应和零状态响应。(1)。(2)。5-17求下述等式所描述的LTI系统
13、的冲激响应和前馈响应。(1)5-18已知系统函数和初始状态如下,求系统的零输入响应。(1),(3),5-22如图5-5所示的复合系统,由4个子系统联接组成,若各子系统的系统函数或冲激响应分别为,求复合系统的冲激响应。5-26如图5-7所示系统,已知当时,系统的零状态响应,求系数a、b、c。5-28某LTI系统,在以下各类情况下起初始状态相同。已知当激励时,其全响应;当激励时,其全响应。(1)若,求系统的全响应。5-29如图5-8所示电路,其输入均为单位前馈函数,求电流的零状态响应。5-42某系统的频度响应,求当输入为下述函数时的零状态响应。(1)(2)5-50
14、求下述象函数的双边拉普拉斯变换。(1)(2)(3)(4)6.4按照下述象函数及所标明的收敛域,求其所对应的原序列。(1),全z平面(2)(3)(4)(5)(6)6.5已知,试借助z变换的性质求下述序列的z变换并标明收敛域。(1)(3)(5)(7)(9)6.8若因果序列的z变换如下,能够应用年率定律?倘若能,求出。(1)(3)6.10求下述象函数的双边逆z变换。(1)(2)(3)(4)6.11求下述象函数的逆z变换。(1)(2)(5)(6)6.13如因果序列,试求下述序列的z变换。(1)(2)6.15用z变换法解下述齐次差分方
15、程。(1)(3)6.17描述某LTI离散系统的差分多项式为已知,求该系统的零输入响应,零状态响应及全响应。6.19图6-2为两个LTI离散系统框图,求各系统的单位序列响应和前馈响应。6.20如图6-2的系统,求激励为下述序列时的零状态响应。(1)(3)6.23如图6-5所示系统。(1)求该系统的单位序列响应。(2)若输入序列,求零状态响应。6.24图6-6所示系统,(1)求系统函数;(2)求单位序列响应;(3)列写该系统的输入输出差分多项式。6.26已知某LTI因果系统在输入时的零状态响应为求该系统的系统函数,并画出它的模拟框图。图6-126-29已知某一阶LTI
16、系统,当初始状态,输入时,其全响应;当初始状态,输入时,其全响应。求输入时的零状态响应。6.31如图6-10所示的复合系统由3个子系统组成,已知子系统2的单位序列响应,子系统3的系统数,当输入时复合系统的零状态响应。求子系统1的单位序列响应。6.33设某LTI系统的前馈响应为,已知当输入为因果序列时,其零状态响应求输入。6.34因果序列满足等式求序列。6.37联通平均是一种用以滤除噪音的简单数据处理方式。当接收到输入数据后,就将本次输入数据与其前3次的输入数据(共4个数据)进行平均。求该数据处理系统的频度响应。6.46如图6-所示为因果离散系统,为输入,为输出。(1)列举该系统的
17、输入输出差分多项式。(2)问该系统存在频度响应否?为何?(3)若基频函数存在,求输入时系统的稳态响应。7.3如图7-5的RC带通混频电路,求其电流比函数及其零、极点。7.7连续系统a和b,其系统函数的零点、极点分布如图7-12所示,且已知当时,。(1)求出系统函数的表达式。(2)写出幅信噪比应的表达式。7.10图7-17所示电路的输入阻抗函数的零点在-2,极点在,且,求R、L、C的值。7.14如图7-27所示的离散系统,已知其系统函数的零点在2,极点在-0.6,求各系数a,b。7.18图7-29所示连续系统的系数如下,判定该系统是否稳定。(1);(2);(3)。7.19
18、图7-30所示离散系统的系数如下,判定该系统是否稳定。(1);(2);(3)。7.20图7-31所示为反馈系统,已知,K为常数。为使系统稳定,试确定K值的范围。7.26已知某离散系统的差分多项式为(1)若该系统为因果系统,求系统的单位序列响应h(k)。(2)若该系统为稳定系统,求系统的单位序列响应h(k),并估算输入时的零状态响应。7.28求图7-36所示连续系统的系统函数。7.30画出图7-40所示的讯号流图,求出其系统函数。解(a)由s域系统框图可得系统的讯号流图如图7-41(a)。流图中有一个回路。其增益为(b)由s域系统框图可得系统的讯号流图如图7-41(b)。流图中
19、有一个回路。其增益为7.32如连续系统的系统函数如下,试用直接方式模拟此系统,画出其方框图。(1)(3)(e)(f)图7-31相应的方框图为图7-31(c)7.33用级联方式和并联方式模拟7.32题的系统,并画出框图。讯号流图为图7-32(a),响应的方框图为图7-32(b)。讯号流图为图7-32(c),响应的方框图为图7-32(d)。(b)(c)(d)分别画出和的讯号流图,将二者级联即得的讯号流图信号与系统答案 张小虹,如图7-50(a)所示,其相应的方框图如图7-50(b)所示。分别画出和和的讯号流图,将两者并联即得的讯号流图信号与系统答案 张小虹,如图7-50(c)所示,其相应的方框图如图7-50(d)所示。7.37图7
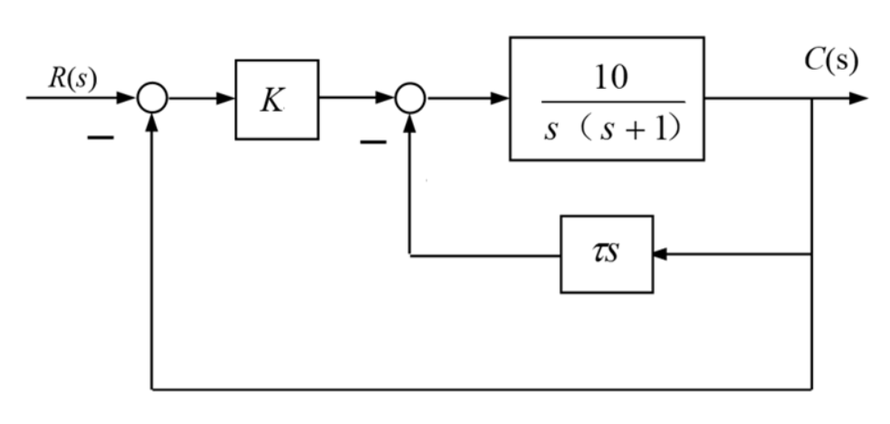
20、-61所示为离散LTI因果系统的讯号流图。(1)求系统函数。(2)列写出输入输出差分多项式。(3)判定该系统是否稳定。7.38在系统的稳定性研究中,有时还应用“罗斯(Routh)判据或准则”,借助它可确定方程的根是否都坐落s左半平面。这儿只说明对二、三阶方程的判据。二阶方程的根都坐落s左半平面的充分必要条件是:;对三阶方程的根都坐落s左半平面的充分必要条件是:。按照上述推论,试判定下述各表达式的根是否都坐落s左半平面。(1)(2)(3)(4)(5)7.38在系统的稳定性研究中,有时还应用“朱里判据或准则”,借助它可确定方程的根是否都坐落单位圆内。这儿只说明对二阶方程的
21、判据。二阶方程的根都坐落z单位圆内的充分必要条件是:。按照上述推论,试判定下述各表达式的根是否都坐落单位圆内。(1)(2)(3)(4)8.1对图8-1所示电路,列写出以、为状态变量x1、x2,以、为输出的状态多项式和输出多项式。8.2描述某连续系统的微分多项式为写出该系统的状态多项式和输出多项式。8.3描述连续系统的微分多项式组如下,写出系统的状态多项式和输出多项式。(1)(2)8.4以x1、x2、x3为状态变量,写出图8-3所示系统的状态多项式和输出多项式。8.7如图8-7所示连续系统的框图。(1)写出以x1、x2为状态变量的状态多项式和输出多项式。(2)为使该系统稳定,常数a,b应满足哪些条件?8.9描述某连续系统的系统函数为画出其直接方式的讯号流图,写出相应的状态多项式和输出多项式。解:将系统函数改写成由此可画出直接方式的讯号流图,如图8-10所示。选定图8-10中积分器的输出作为状态变量。由图8-10可写出如下等式将式和式写成矩阵方式,得状态多项式将式写成矩阵方式,得输出多项式8.12某离散系统的讯号流图如图8-13所示。写出以x1(k)、x2(k)为状态变量的状态多项式和输出多项式。8.13如图8-14所示离散系统,状态变量x1、x2、x3如图8-14所示。列举系统的状态多项式和输出多项式。









